Question

A person travelled a distance of 3 km along a straight line in the North direction. Then he travelled 2 km in the west direction and then 5 km in the south direction. The magnitude of the displacement of this person would be _ _ _ _ _ _ _ _.
A. \[2\sqrt 2 \,{\text{km}}\]
B. \[3\sqrt 2 \,{\text{km}}\]
C. \[4\sqrt 2 \,{\text{km}}\]
D. \[10\,{\text{km}}\]

Answer 1

Hint: Denote the direction along the East as \[\hat i\] and the direction along the North as \[\hat j\]. Express the final position of the person using the formula for position vector. Determine its magnitude to get the displacement of the person.

Formula used:
\[d = x\hat i + y\hat j\]
Here, x is the x-coordinate and y is the y-coordinate.

Complete step by step answer:
Let the direction along the East is \[\hat i\] and the direction along the North is \[\hat j\]. We can map the journey of the person as shown in the figure below.

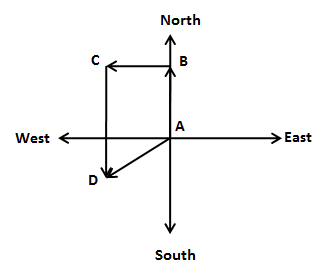
In the above figure, the person has started its journey from the point A and D is the final point of his journey. The distance AD is the displacement of the person.
Let’s express the displacement of the person in the vector form as follows,
\[AD = x\hat i + y\hat j\]
Here, x is the total displacement along the East and West direction and y is the total displacement along the North and South direction.
Therefore,
\[AD = \left( { - 2} \right)\hat i + \left( {3 - 5} \right)\hat j\]
\[ \Rightarrow AD = - 2\hat i - 2\hat j\]
Now, let’s determine the magnitude of the displacement as follows,
\[\left| {AD} \right| = \sqrt {{x^2} + {y^2}} \]
\[ \Rightarrow \left| {AD} \right| = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 2} \right)}^2}} \]
\[ \Rightarrow \left| {AD} \right| = \sqrt 8 \]
\[ \Rightarrow \left| {AD} \right| = 2\sqrt 2 \,{\text{km}}\]

Therefore, the displacement of the person is \[2\sqrt 2 \,{\text{km}}\].


So, the correct answer is “Option A”.

Note:
Students must remember the important difference between distance and displacement. The distance is the total distance travelled by the body along every direction that he travels but the displacement is the difference in the final position and initial position of the body. in the given question, the distance travelled by the person is \[3 + 2 + 5 = 10\,{\text{km}}\]but the displacement is \[2\sqrt 2 \,{\text{km}}\].