Question

A person standing in an open ground hears the sound of a jet airplane coming from north at angle ${60^ \circ }$ with ground level. But he finds the airplane vertically above his position. If v is the speed of sound, the speed of the plane is:
$A. \dfrac{{2v}}{{\sqrt 3 }}$
$B. v$
$C. \dfrac{v}{2}$
$D. \dfrac{{\sqrt 3 }}{2}v$

Answer 1

Hint: The distance travelled by sound will be equal to the distance travelled by the jet airplane. Therefore, if we find the velocity, we will be able to solve the given problem.

Complete step-by-step answer:
Let us consider the angle between the man and the jet airplane is ${60^ \circ }$
Let us assume that the distance between the man and the jet airplane is $d$.
The horizontal distance between the man and jet airplane \[d = \cos {60^ \circ }\]
As the value of the angle of the distance between the man and the jet airplane is \[\cos {60^ \circ }\]. We can convert the \[\cos {60^ \circ }\] in numbers we get,
\[ \Rightarrow d = \cos {60^ \bullet }\]
\[ \Rightarrow \dfrac{1}{2}\]
Let us consider that the jet airplane is flying top of the man and the distance between the triangle and the man forms a triangle shape. Angle between the jet plane and the man is ${60^ \circ }$. We take $\cos $ as because the jet is flying high adjacent to the man and since $\cos $ is adjacent side by hypotenuse we are considering $\cos $ instead of other angles.

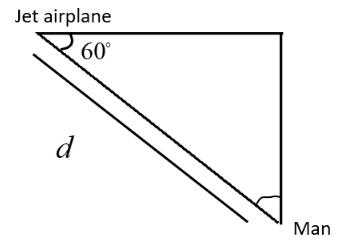
Therefore, the horizontal distance between the man and jet airplane \[d \times \left( {\dfrac{1}{2}} \right)\]\[ = \dfrac{d}{2}\]
 Again, we can say that the distance travelled by sound is equal to the distance between the man and the airplane, that is,
Distance travelled by sound \[ = \dfrac{d}{2}\]
Since, in the question it is given that the velocity of sound is v,
The time taken for sound to travel \[ = \dfrac{d}{v}\] seconds
The sound travels a distance \[ = \dfrac{d}{2}m\]= distance travelled by the jet airplane
Time taken by the airplane to cover $\dfrac{d}{2}$ distance will be equal to \[\dfrac{d}{v}\] times time taken by sound to travel
When we divide the distance covered by a jet plane with respect to the time taken by the plane to cover the distance we get the velocity.
 Velocity of the jet plane
 \[ \Rightarrow \dfrac{{\dfrac{d}{2}}}{{\dfrac{d}{v}}}\]
\[\therefore \dfrac{v}{2}\]

Hence the correct option is (C).

Note: This question uses the concept of relative motion. When we consider a body to have some velocity, then it has to be with respect to a frame of reference. In most cases of everyday life, this frame of reference is taken as the ground or Earth. Relative velocity of object 1 with respect to object 2 is the rate of change of the position of object 1 to object 2. Do not confuse between the distance traveled by the plane and the horizontal distance between the man and the jet airplane.