Question

A person standing between two vertical cliffs and $480{\text{ }}m$ from the nearest cliff shouts. He hears the first echo after $3{\text{ }}s$ and the second echo ${\text{2 }}s$ later. Calculate:
(i) The speed of sound.
(ii) The distance of the other cliff from the person.

Answer 1

Hint: We have to consider a distance from which the person is standing from the cliffs. The echo will be heard faster from that cliff which is closer to the person. By using the given information, we will find the speed of sound from the relation between distance, time and velocity. Again, after getting the value of speed of sound we will eventually find the distance between the person and the other cliff.

Complete step by step answer:

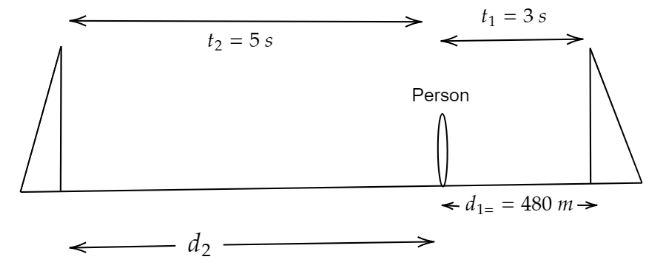
The cliff which is nearer to the person be ${d_1}$ which has the distance of $480{\text{ }}m$ between them. Hence, the time required ${t_1}$ to hear echo due to this vertical cliff is less which is $3{\text{ }}s$. The total distance covered by the sound wave is $2{d_1}$. Let the velocity of the sound wave be $v$. So, the speed of the sound,
$v = \dfrac{{2{d_1}}}{{{t_1}}} \\
\Rightarrow v = \dfrac{{2 \times 480}}{3} \\
\therefore v = 320{\text{ }}\dfrac{m}{s}$

Therefore, the speed of the sound is $320{\text{ }}\dfrac{m}{s}$.

(ii) The speed of the sound remains constant as the medium does not change.Let the distance between the other cliff and the person be ${d_2}$. Total time ${t_2}$ required to hear the echo due to another cliff is $\left( {3 + 2} \right) = 5{\text{ }}s$. Hence, from the relation between distance, time and velocity we get.
${d_2} = v \times {t_2} \\
\Rightarrow {d_2} = 320 \times 5 \\
\therefore {d_2} = 1600{\text{ }}m$

Therefore, the distance of the other cliff from the person is $1600{\text{ }}m$.

Note: It must be noted that echo is defined as the bouncing back of a sound wave when it structs an object. Echo is heard when a person is at a long distance from the reflecting object and the space between the reflecting object and the source is almost vacant.