Question

A person standing at the junction of two straight paths represented by the equation 2x – 3y + 4 = 0 and 3x + 4y – 5 = 0 want to reach the path whose equation is 6x – 7y + 8 = 0 in the least time. Find the equation of the path he should follow.

Answer 1

Hint: Now first we will find the point of intersection of 2x – 3y + 4 = 0 and 3x + 4y – 5 = 0. Now a person wants to reach the path 6x – 7y + 8 = 0. Now we can arrange the equation in slope form and hence find the slope of the line. Now we know that the line shortest path from the path to the point of intersection will be perpendicular to the line 6x – 7y + 8 = 0 and we also know that the product of slopes of perpendicular lines is -1. Hence we have the slope of the required line. Now we will write the equation of line in slope intercept form.

Complete step by step answer:

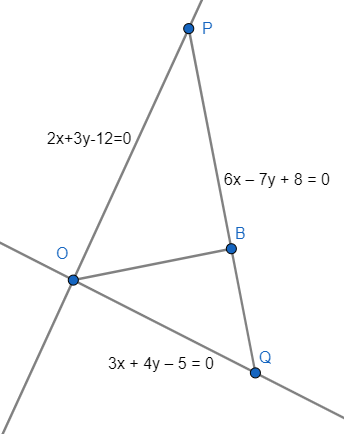
Now let us say that O is the intersection of lines 2x – 3y + 4 = 0 and 3x + 4y – 5 = 0
Now consider the line 2x – 3y + 4 = 0
Multiplying the whole equation by 4 we get,
8x – 12y + 16 = 0………………………… (1)
Now consider the line 3x + 4y – 5 = 0.
Multiplying the whole equation by 3 we get 9x + 12y – 15 = 0 ………………………. (2)
Now adding equation (1) and equation (2) we have 9x + 8x + 16 – 15 = 0.
Hence we get $x=\dfrac{-1}{17}$ .
Now substituting the value of x in equation 2x – 3y + 4 = 0 we get,
$\begin{align}
  & 2\left( \dfrac{-1}{17} \right)-3y+4=0 \\
 & \Rightarrow \dfrac{-2}{17}+4=3y \\
 & \Rightarrow \dfrac{-2+4\times 17}{17}=3y \\
 & \Rightarrow \dfrac{-2+68}{17\times 3}=y \\
 & \Rightarrow y=\dfrac{66}{51} \\
 & \Rightarrow y=\dfrac{22}{17} \\
\end{align}$
Hence we get $O\left( x,y \right)=\left( \dfrac{-1}{17},\dfrac{22}{17} \right)$ .
Now consider the equation of line PQ, 6x – 7y + 8 = 0
Rearranging the terms we get $y=\dfrac{6x}{7}+\dfrac{8}{7}$ .
Now comparing the line with the equation $y=mx+c$ we get the slope of line $m=\dfrac{6}{7}$
Now we know that OB is perpendicular to PQ since the shortest path connecting the point and a line is perpendicular drawn from the line. And the product of slope of perpendicular lines is -1
Hence slope of line OB is $\dfrac{-7}{6}$ .
Now we have the slope of line is $\dfrac{-7}{6}$ and the line passes through point $\left( \dfrac{-1}{17},\dfrac{22}{17} \right)$
Hence the equation of line in slope point form $y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)$ is
Hence we get the equation of the line OB is
$\begin{align}
  & y-\dfrac{22}{17}=\dfrac{-7}{6}\left( x-\dfrac{\left( -1 \right)}{17} \right) \\
 & \Rightarrow \dfrac{17y-22}{17}=\dfrac{-7\left( 17x+1 \right)}{17\times 6} \\
 & \Rightarrow 6\left( 17y-22 \right)=-7\left( 17x+1 \right) \\
 & \Rightarrow 102y-132=-119x-7 \\
 & \Rightarrow 119x+102y=125 \\
\end{align}$

Hence the required equation of line is 119x + 102y = 125.

Note: Now we can also solve this question by first finding the foot of perpendicular from the point O to the line 6x – 7y + 8 = 0. Now this foot of perpendicular is nothing but the point B hence we can easily find the equation of OB by using the equation of line in two point form.