Question

Where should a person stand straight from the pole of a convex mirror of focal length 2.0m on its axis so that the image formed becomes half of his original height?
A. -6.0 m
B. -4.0 m
C. -0.5 m
D. -2.0 m

Answer 1

Hint:We will use the formula for magnification in a convex mirror to find the desired relation between the distance of man from the mirror and the distance from the mirror where the image is formed and use it in the mirror formula to get the value of the distance of man from the mirror.

Formula used:
Mirror formula
$\dfrac{1}{v}+\dfrac{1}{u}=\dfrac{1}{f}$
magnification in a convex mirror
$M=\dfrac{v}{u}$

Complete step-by-step solution:
First, we will find the relation between the distance of man from mirror and the distance from mirror where the image is formed. We are given that the image is half of the height of the man. So, magnification is 0.5
$M=\dfrac{v}{u}=0.5\Rightarrow v=0.5u$
We will now use this relation in the mirror formula.
$\begin{align}
  & \dfrac{1}{v}+\dfrac{1}{u}=\dfrac{1}{f} \\
 & \Rightarrow \dfrac{1}{f}=\dfrac{1}{0.5u}+\dfrac{1}{u}=\dfrac{2}{u}+\dfrac{1}{u}=\dfrac{3}{u}=\dfrac{1}{-2} \\
 & \Rightarrow u=-6m \\
\end{align}$

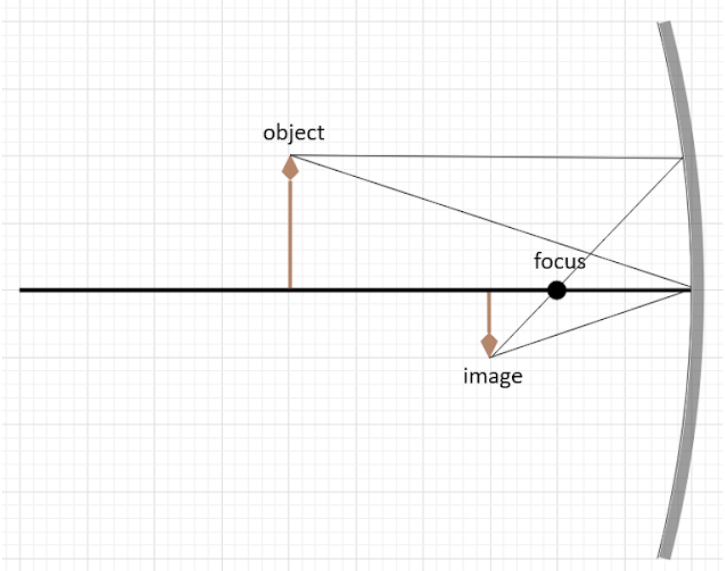
1 unit = 1 metre
Thus, we get that when the man stands at a distance of 6m from the pole of a convex mirror of focal length 2.0m on its axis so that the image formed becomes half of his original height. The negative sign denotes that the object must be kept on the left of the mirror. And according to the sign convention used, that will be the same side as the focus of the mirror. Hence, the correct option is A, i.e. -6.0 m.

Note: Students must observe a strict sign convention when solving the problems related to mirrors and lenses. Here we have used the most commonly used sign convention and thus we have also used the formulas directly. The sign convention used here is that distances on the left of the mirror are negative and on the right are positive and the object is always kept on the left.