Question

A person rows a boat in water with a speed $4m/s$, water in the river is flowing at a speed of $2m/s$. If the person rows the boat perpendicular to the direction of the flow, find the resultant velocity of the boat and time taken by the boat to cross the river, if the width of the river is $400\;m$.

Answer 1

Hint: Since the boat is moving on a river which is flowing, then we can say that, the velocity of the river acts as an hindrance for the movement of the boat. For the boat to cross the river, clearly it must overcome the velocity of the river.

Formula used: $v_{r}=\sqrt{v_{b}^{2}+v_{w}^{2}}$ and $vel=\dfrac{dist}{time}$

Complete step by step answer:
Let us consider that boat starts from a point $O$ as shown in the figure. Let the velocity of the boat be $v_{b}=4m/s$ and the velocity of the $v_{w}=2m/s$. Also given that the width of the river is $d=400\;m$.
Let us say that the boat from $O$ reaches the perpendicular point $A$ in the absence of the $v_{w}$. Due to the velocity of the river, $v_{w}$, clearly, this hinders the movement of the boat and thus the boat from $O$ reaches $B$ , instead of $A$, which is inclined at an angle $\theta$ with respect to $O\;A$

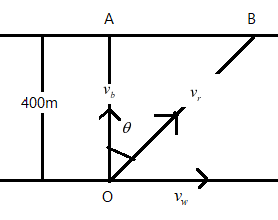
Let $v_{r}$ be the resultant vector. Then from the parallelogram law of vector addition, we can say that figure we can say that the resultant velocity $v_{r}$
Then the magnitude of the resultant vector is given as $v_{r}=\sqrt{v_{b}^{2}+v_{w}^{2}}$
$\implies v_{r}=\sqrt{4^{2}+2^{2}}=\sqrt{16+4}=\sqrt{20}=2\sqrt5 m/s$
Also we know that, $vel=\dfrac{dist}{time}$
Given that the width of the river is $d=400\;m$ and the velocity acting on the same axis is $v_{b}$
Then, $t=\dfrac{400}{4}=100s$

Thus the velocity of the resultant is $v_{r}=2\sqrt5$ and the time taken $t=100s$

Note: This sum may seem very hard at first glance, but if one draws the diagram and labels the diagram correctly, it is easy to solve the question. The question uses only the basic parallelogram law of vector addition and speed formula.