Question

A person is $x$ meters away from a bus. The bus begins to move constant acceleration $a.$ The person started running at a constant speed $u$ to catch the bus.
The speed of the person so that he may catch the bus is
A. $\sqrt {3ax} $
B. $\sqrt {2ax} $
C. $\sqrt {ax} $
D. $\sqrt {\dfrac{{2a}}{x}} $

Answer 1

Hint: Use the laws of motion to calculate the time taken for man to catch the bus. Form an equation in terms of time and velocity and then use the concept that the man is running with constant velocity to solve the question.

Formula used:
$s = ut + \dfrac{1}{2}a{t^2}$
Where,
$s$ is displacement
$u$ is initial velocity
$a$ is acceleration
$t$ is time

Complete step by step answer:
Observe the diagram

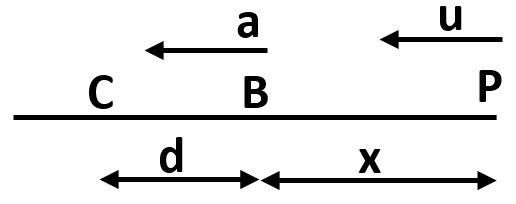
Let P be the point where the person is standing. B be the initial position of the bus.
The distance between the bus and the person is $x$
When the bus starts to move, the person starts running towards the bus. So, by the time, the person catches the bus, the bus would have moved ahead to some point, say C.
The velocity, with which, the person is running towards the bus is $u$
The bus starts to move with the constant acceleration $a$
Let the time taken by the person to catch the bus be $t$
Let the bus moved to the point C in that time by covering a distance $d$
Now, we know that,
$s = ut + \dfrac{1}{2}a{t^2}$
Where,
$s$ is displacement
$u$ is initial velocity
$t$ is time taken to cover the displacement $s$
$a$ is acceleration.
Then, using above formula, we can write, the distance covered by the bus as
$d = \dfrac{1}{2}a{t^2}$ (since, initial velocity of the bus is zero)
Since, the bus covers distance $d$, the man will have to cover the distance, $d + x$ to catch the bus.
Therefore, again using the formula of law of motion given above, we can write
$d + x = ut + \dfrac{1}{2}a{t^2}$
$ \Rightarrow d + x = ut$ (since, the person is running with constant velocity, acceleration of the person will be zero)
By substituting the value of $d$ in this equation, we get
$\dfrac{1}{2}a{t^2} + x = ut$
By dividing both the sides by $t$ and re-arranging it, we get
$u = \dfrac{1}{2}at + \dfrac{x}{t}$ . . . (1)
Since, the acceleration of the person is zero. We can write,
$\dfrac{{du}}{{dt}} = 0$
$ \Rightarrow \dfrac{{du}}{{dt}} = \dfrac{1}{2}a - \dfrac{x}{{{t^2}}} = 0$
$ \Rightarrow \dfrac{x}{{{t^2}}} = \dfrac{a}{2}$
By taking reciprocal and then, moving $x$ to the other side by cross multiplication, we get
${t^2} = \dfrac{{2x}}{a}$
$t = \sqrt {\dfrac{{2x}}{a}} $
By substituting the values of $t$ in equation (1), we get
$u = \dfrac{1}{2}a\sqrt {\dfrac{{2x}}{a}} + \dfrac{x}{{\sqrt {\dfrac{{2x}}{a}} }}$
By simplifying it, we get
$u = \sqrt {\dfrac{{ax}}{2}} + \sqrt {\dfrac{{ax}}{2}} $
$ \Rightarrow u = 2\sqrt {\dfrac{{ax}}{2}} $
$ \Rightarrow u = \sqrt {2ax} $
Therefore, the speed with which the man will need to run will be $\sqrt {2ax} $
Therefore, from the above explanation, the correct answer is, option (B)

Note:
To solve this question, it is important to understand that the bus will also cover some distance, when the man is running behind it. You need to observe that the initial velocity of the bus will be zero as it is starting from the rest and the acceleration of the man will be zero as he is running with a constant velocity.