Question

A person is in front of a vertical mountain, fires a bullet, and hears its echo after a time of 3 seconds. The person walks a distance ‘d’ towards the mountain, then fires another bullet and hears its echo after 2 seconds. If the velocity of sound in air is 340 centimeters per seconds, the value of ‘d’ is:
A. 85 cm
B. 170 m
C. 255 m
D. 340 m

Answer 1

Hint:Here in the question, we need to determine the distance traveled by the man towards the mountain so that when he fires the second bullet, he hears the echo after 2 seconds. For this, we will use the very basic distance formula, which is $d = vt$ where d is the distance, v is the velocity, and t is the time.

Complete step by step answer:

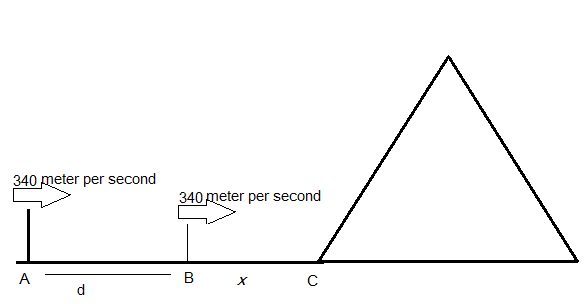
Following the distance formula as to $d = vt - - - - (i)$ where d is the distance, v is the velocity, and t is the time taken in the given scenario.

$(d + x)$ is the initial total distance between the man and the mountain such that the velocity of firing is 340 meters per second and 3 seconds is the time when he hears the sound back so, the total distance would be 2 times of $(d + x)$.

Following equation (i), we get,
$
  2\left( {d + x} \right) = vt \\
  d + x = \dfrac{{340 \times 3}}{2} \\
   = 510 - - - - (ii) \\
 $

Again, when the man fires the bullet from point B (from the figure), the distance is $2x$, velocity is 340 meters per second, and 2 seconds is the time when he hears the sound back. So, following the equation (i), we get:
$
  d = vt \\
  2x = 340 \times 2 \\
  x = 340{\text{ cm}} - - - - (iii) \\
 $

Substituting equation (iii) in the equation (ii), we get:

$
  d + x = 510 \\
  d + 340 = 510 \\
  d = 170{\text{ cm}} \\
 $

Hence, the man moved towards the mountain by 170 meters.

Option B is correct.

Note:Students should be careful while using the total distance between the man and the mountain. Here, as the sounds come back to the man so that he can hear the echo so, the total distance should be twice.