Question

A person draws water from a \[5m\] deep well and bucket of mass \[2kg\] of capacity \[8litre\] by a rope of mass \[1kg\] . What is the total work done by the person? $\left( {{\text{Assume}}\,\,g = 10m/{{\sec }^2}} \right)$

Answer 1

Hint: Work is said to be done on a body by a force, when the force acting on the body produces a displacement in any direction except in a direction perpendicular to direction of force. It measures the energy transfer that takes place. Work is a scalar product. There are positive work done, negative work done and zero work done.
Formula:
Work done,
\[W = F \cdot S\]
Where
$F$ , is the force
And $S$ , is the displacement
Force can be written as \[f = mg\]
Where $m$ , is the mass of body and $g$ is the acceleration of body

Complete Step by Step Answer:
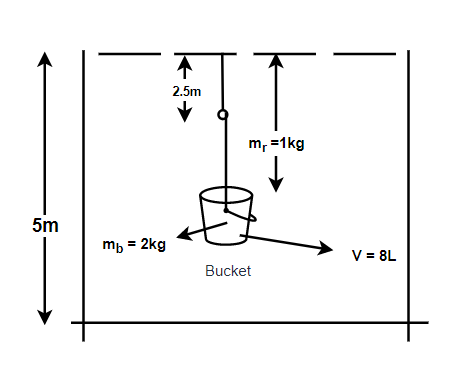
According to question, the height of well, \[h = 5cm\] , Mass of bucket, \[{m_b} = 2kg\] , Mass of rope, \[{m_r} = 1kg\] and Volume of bucket, \[V = 8litre\]

We know that, Density of water is \[1000kg{m^{ - 3}}\] or \[1gc{m^{ - 3}}\]
As density = mass/ volume
To convert liters to kilogram, we will use above formula of density to calculate mass of water in \[kg\] which is ${\text{Mass}}\,\,{\text{ = }}\,\,{\text{Density \times Volume}}$
$ \Rightarrow 1\dfrac{{kg}}{{{m^3}}} \times 8{m^3} = 8kg$
Mass of water is equal to \[8kg\]
Total mass of bucket and water, \[m = \left( {8 + 2} \right)kg = 10kg\]
So, Total work done \[\left( w \right)\] will be equal to, Work done to lift bucket \[{W_o}\] and the addition of Work done to lift rope \[{W_r}\]
Work done to lift bucket, ${W_ \circ } = Mgh = 10 \times 10 \times 5 = 500J$
As use know that work done to lift rope will depend on Centre of mass of rope which is at \[2.5m\]
(We must consider the bucket to be of negligible height)
Then, only the Centre of mass of rope will lie at \[2.5m\] which is half the height.
Work done to lift rope \[\left( {{W_r}} \right) = {M_r}g\dfrac{h}{2} = 1 \times 10 \times 2.5 = 25J\]
So, total work done, $W = 500 + 25 = 525J$

Therefore, option \[\left( b \right)\] is correct answer

Note: The unit of work done is Joule \[\left( J \right)\] . Also, if more than one force is acting on a body, the work done by all the forces together is the sum of work done by each of them separately.