Question

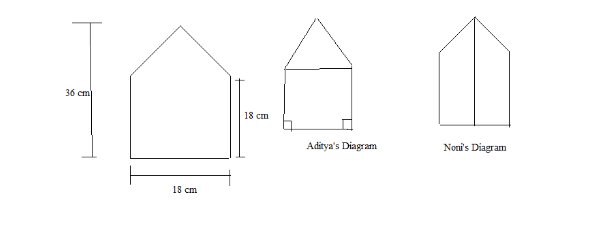
A pentagon is divided in two different ways by Aditya and Noni as shown in the figure. Find the area of this pentagon using both ways.

Answer 1

Hint: A pentagon has a plane figure with five straight sides and 5 angles as it can be seen in figure. Aditya has drawn an imaginary line which divides the pentagon into a triangle and a square, so it is clear that we will find out the area of the triangle and the area of the square separately and add them up to get the total area of the given pentagon. In Noni’s diagram, an imaginary line has been drawn such a way that the line bisects the pentagon in two equal trapeziums. We can find the area of one trapezium and double it to get the area of the whole pentagon because the trapeziums are identical.

Complete step-by-step answer:
For Aditya’s diagram
Length of side of the square = \[18\text{ }cm\]
Length of the base of the triangle = \[18\text{ }cm\]
Height of the triangle = \[18\text{ }cm\]
For Noni’s diagram:
Length of one parallel side of the trapezium = \[18\text{ }cm\]
Length of another parallel side of the trapezium = \[\text{36 }cm\]
Distance between the parallel sides of the trapezium = \[\text{9 }cm\]
Step 1: To calculate the area of the pentagon by using Aditya’s way:
\[\Rightarrow Area\text{ }of\text{ }pentagon\text{ }=Area\text{ }of\text{ }triangle\text{ }+\text{ }area\text{ }of\text{ }square\] = \[\dfrac{1}{2}\times base\times height+{{(side)}^{2}}\]
= \[[\dfrac{1}{2}\times 18\times 18+{{(18)}^{2}}\,]\text{ }c{{m}^{2}}\]
= \[162\text{ }+\text{ }324\text{ }c{{m}^{2}}\]
= \[486\text{ }c{{m}^{2}}\]

Step 2:To calculate the area of the pentagon by using Noni’s way:
\[\Rightarrow Area\text{ }of\text{ }pentagon\text{ }=2\times Area\,of\,trapezium\]
= \[2\times [\dfrac{1}{2}\times Sum\,of\,parallel\,side\times Distance\,between\,parallel\,side]\]
= \[2\times [\dfrac{1}{2}\times (18+36)\times 9]\,c{{m}^{2}}\]
= \[2\times [\dfrac{1}{2}\times 54\times 9]\,c{{m}^{2}}\]
= \[486\text{ }c{{m}^{2}}\]

Note: Students often get confused between the heights of the triangle and the side of the triangle. Also, not to be confused with the sum of the sides in trapezium, the parallel sides are meant to be added and multiplied with the distance between them.