Question

A pentagon can be divided into how many triangles by drawing all of the diagonals from one vertex?

Answer 1

Hint: In geometry a pentagon is a polygon having 5 sides, and 5 internal angles, also triangles are polygons having 3 sides as well as internal angles. To solve the given question, we have to fix one of the vertices of a pentagon. Then, draw lines from the fixed vertex to the other four vertices, and count the number of triangles that can be formed. To make things simple, we will use a regular polygon for this. A regular polygon is a special polygon having all sides equal.

Complete step-by-step solution:
We are asked to count the number of triangles that can be found using the vertices of a pentagon. To solve the given question, we will have to fix one of the vertices of the pentagon. Then, draw lines from the fixed vertex to the other four vertices, and count the number of triangles that can be formed.
We are given the pentagon,

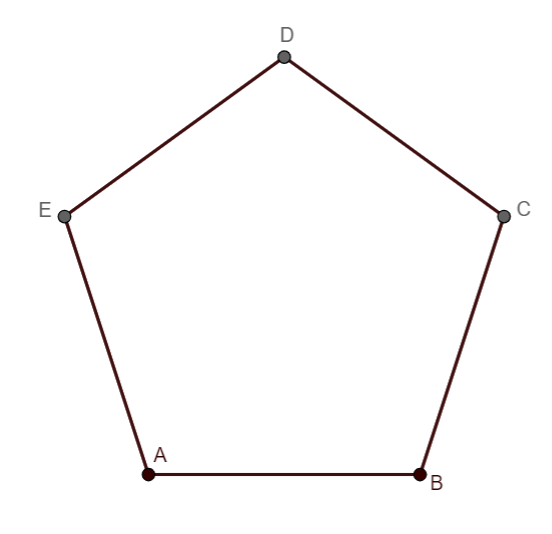
We will fix the vertex A, and draw lines joining other vertices with it. By doing this, we get a figure as follows,

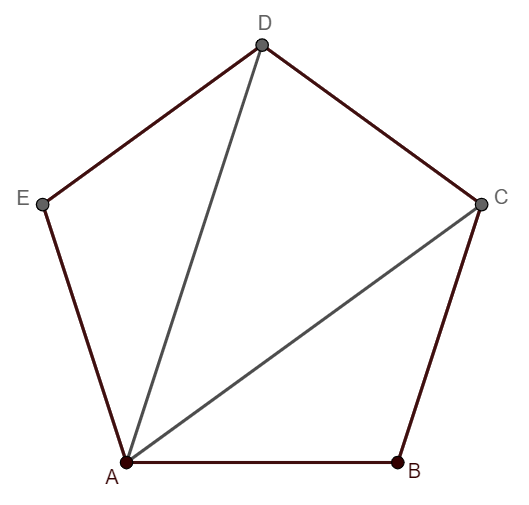
Thus, we are getting three triangles by drawing the lines that join the fixed vertex A with the vertices C, and D. The names of the triangles are \[\Delta ABC,\Delta ADC,\Delta AED\].

Note: Here, we join the vertex A with only two other vertices. The reason of this is as follows:
The pentagon has a total 5 vertices, we have fixed one vertex so there are four remaining. Out of the four vertices, two vertices B and E are adjacent to the fixed vertex. Hence, by joining them we will get a line. Thus, excluding these four, only two vertices remain.