Question

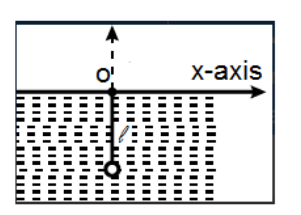
A pendulum of length \[l\] is free to oscillate in the vertical plane above point \[O\]. An observer is viewing the bob of the perpendicular directly from above. The pendulum is performing small oscillations in water (refractive index is \[\mu \]) about its equilibrium position. The equation of trajectory of bob as seen by observer is –

A. ${\mu ^2}{x^2} + {y^2} = {l^2}$
B. $\dfrac{{{x^2}}}{{{l^2}}} + \dfrac{{{y^2}}}{{{\mu ^2}{l^2}}} = 1$
C. ${x^2} + {y^2} = {\left( {\dfrac{l}{\mu }} \right)^2}$
D. $\dfrac{{{x^2}}}{{{l^2}}} + \dfrac{{{y^2}}}{{{{\left( {\dfrac{l}{\mu }} \right)}^2}}} = 1$

Answer 1

Hint:In order to solve this question, we are going to first consider a configuration for the bob and then using the Snell’s law, we are going to form the further equations by finding the values of the sine and the cosine functions from the figure that is constructed. And finally get the required equation.

Formula used:
According to the Snell’s law,
\[\mu \sin i = \sin r\]
where, the two angles on the L.H.S and R.H.S are the angles of incidence and reflection respectively.

Complete step by step answer:
Let us consider the configuration of the bob in the following way: let \[\left( {x,y} \right)\] be the coordinates of the bob with respect to air, Let \[\left( {x',y'} \right)\] be the coordinates of the bob with respect to water.Let length of the pendulum bob be \[{l_0}\] while let \[l\] be the length of the pendulum bob as seen through water,

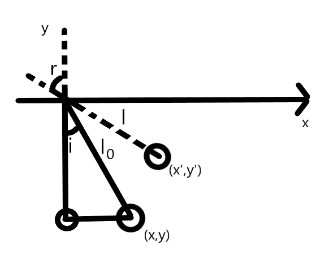
Now, according to the Snell’s law,
\[\mu \sin i = \sin r\]
Where,
$\sin i = \dfrac{x}{{{l_0}}} \\
\Rightarrow \sin r = \dfrac{{x'}}{l} \\
\Rightarrow \cos i = \dfrac{y}{{{l_0}}} \\
\Rightarrow \cos r = \dfrac{{y'}}{l}$
Now, we get
\[x' = \dfrac{{\mu xl}}{{{l_0}}}\]
Also, \[\mu \sqrt {1 - \dfrac{{{y^2}}}{{l_0^2}}} = \sqrt {1 - \dfrac{{y{'^2}}}{{{l^2}}}} \]
Squaring this equation on both sides, we get
$y' = {\mu ^2}\left( {1 - \dfrac{{{y^2}}}{{l_0^2}}} \right) = \left( {1 - \dfrac{{y{'^2}}}{{{l^2}}}} \right) \\
\Rightarrow y' = \sqrt {{l^2}\left( {1 - {\mu ^2}\left( {1 - \dfrac{{{y^2}}}{{l_0^2}}} \right)} \right)} \\$
We know that, \[x{'^2} + y{'^2} = {l^2}\]
This implies that,
$\dfrac{{{\mu ^2}{x^2}{l^2}}}{{l_0^2}} + {l^2}\left( {1 - \left( {{\mu ^2} - \dfrac{{{y^2}}}{{l_0^2}}} \right)} \right) = {l^2} \\
\Rightarrow \dfrac{{{\mu ^2}{x^2}}}{{l_0^2}} + 1 - {\mu ^2} + \dfrac{{{y^2}}}{{l_0^2}} = 1 \\
\therefore \dfrac{{{x^2}}}{{l_0^2}} + \dfrac{{{y^2}}}{{{{\left( {\dfrac{{{l_0}}}{\mu }} \right)}^2}}} = 1$
Thus, the required equation is \[\dfrac{{{x^2}}}{{l_0^2}} + \dfrac{{{y^2}}}{{{{\left( {\dfrac{{{l_0}}}{\mu }} \right)}^2}}} = 1\] .

Hence, option D is the correct answer.

Note:It is important to note that while constructing the figure for the pendulum that is oscillating in the water, we are going to take the required positions of oscillation and the respective lengths at that point. The angles and the lengths give further equations for finding the final result.