Question

A pendulum is oscillating about its mean position in vacuum. It has:
A. Only kinetic energy
B. Maximum kinetic energy at extreme position
C. Maximum potential energy as its mean position
D. Sum of kinetic energy and potential energy remains constant throughout the motion.

Answer 1

Hint: Pendulum is a structure where one end of a string is attached to one fixed point and another end is attached to a ball. When we pull the ball to any one side and leave it, the ball moves in a to and fro motion, which are called oscillations. We would use the law of conservation of energy to solve this question.

Complete step by step answer:
Observe the diagram.

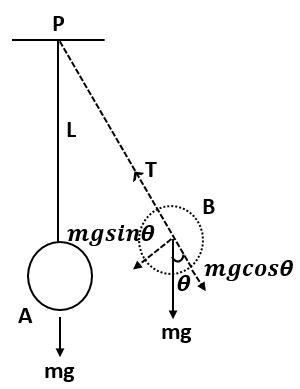
Let a string of length $L$ is attached to a fixed point $P$ from one end and is attached to a ball to the other end.
If no force is applied on the ball, then it will stay at point $A$ due to gravity. This point $A$ is called the mean position of the pendulum.
Now, let us say that we take the pendulum to a position $B$. This position $B$ is called the extreme position of the pendulum.
At point $B$:
We know that the force applied on a pendulum is $F = mg$, due to the gravity of earth. This force will be applied in the downward direction making angle $\theta $ with the string $L$. If we resolve the force, $F$ in two components along the direction of string and along the direction perpendicular to the string. The two components would be $mg\cos \theta $ and $mg\sin \theta $ as shown in the figure. The tension $T$ acting on the string will be exactly equal and opposite to the component $mg\cos \theta $.
Hence, $T$ and $mg\cos \theta $ will cancel each other and the net force acting on the ball will be
$F = - mg\sin \theta $
Negative sign indicates the direction of the force which is trying to take the ball to its original position.
From the above discussion we can conclude that the motion of the pendulum will be in left and right direction (to and fro motion) until a pendulum comes to a stop. This ball will have some energy in it. That energy will be kinetic energy (when the ball is in motion) and potential energy (when the ball is at rest).
The sum of both the energies is total energy
$\therefore T.E = P.E + K.E$
Since, once we leave the ball, we are not adding any extra force to it. Therefore, the total energy of the system will be constant.

Therefore, from the above explanation the correct option is (D) Sum of kinetic energy and potential energy remains constant throughout the motion.

Additional Information:
Potential energy is the energy that is stored in the object when it is at the position of rest. So, when the ball is at the extreme position $B$, the potential energy will be maximum. Because at $B,$ the ball will be at rest (momentarily) before changing its direction of motion.
Hence, option (C) is incorrect. Kinetic energy is the energy that the ball has when it is in motion. At the extreme position $B,$ the ball would change its reaction of motion. Hence, it would come to half at $B.$ That means, at $B,$ the velocity of the ball, is zero. Hence, at an extreme position, kinetic energy will be zero. Therefore, option (B) is incorrect. Clearly, pendulums have kinetic energy and potential energy.
Therefore, option (A) is wrong.

Note:This question was solved only on the basis of logic. To develop such a logic, you need to know the definitions and their meaning. Having a good command over basics helps to solve such questions with ease. Remember, basic undertaking is the foundation on which you will say the structure of knowledge.