Question

A pendulum having a bob mass $m$ is hanging in a ship sailing along the equator from east to west. When the strip is stationary with respect to water, the tension in the string is $T_{0}$. The difference between $T_{0}$ and earth attraction on the bob is:
$\begin{align}
  & A.\dfrac{mg+m{{\omega }^{2}}R}{2} \\
 & B.\dfrac{m{{\omega }^{2}}R}{3} \\
 & C.\dfrac{m{{\omega }^{2}}R}{2} \\
 & D.m{{\omega }^{2}}R \\
\end{align}$

Answer 1

Hint: We know that the time period $T=2\pi \sqrt{\dfrac{L}{g}}$ where $L$ is the length of the simple pendulum and $g$ is the acceleration due to gravity. Due to the rotation of the earth, the pendulum experiences a centripetal force, pulling the pendulum towards the earth.
Formula used: $T_{0}=mg+m\omega^{2}R$

Complete step-by-step solution:
Let us assume that the earth rotates along its axis with an angular velocity $\omega$. Given that the mass of the pendulum is $m$. Let the $L$ is the length of the simple pendulum. Let$\theta$ be the angle made by the pendulum at the point of contact.
Now the pendulum experiences tension $T_{0}$, which acts radially to the pendulum, along the lengths of the pendulum.
The pendulum also experiences a normal force that is given by \[mg\] and a centripetal force which is given by $CF=m\omega^{2}R$ where $R$ is the radius of the earth. Taking the components we get $mgsin\theta$ and $mgcos\theta$

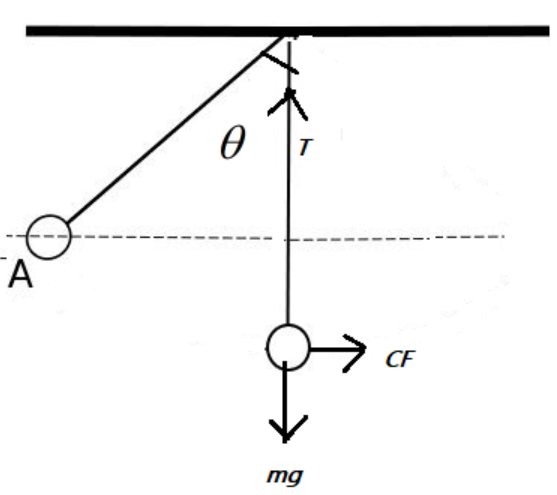
We now form the free body diagram that the net force acting along the positive y-axis is equal to the net force acting along the negative y-axis. Then we can say the tension $T_{0}=mg+m\omega^{2}R$.
Then the difference between the $T_{0}$ and earth attraction on the bob will be $T_{0}-mg=m\omega^{2}R$.
Hence the difference between the $T_{0}$ and earth attraction on the bob will be $m\omega^{2}R$
Thus the answer is D. $m\omega^{2}R$.

Note: This might seem like a complex question but it can be solved easily if the concept of centripetal force and the formulas are known. This question is asked frequently. To understand the question, students are suggested to draw the free body diagram of the pendulum.