Question

A peacock is sitting on the top of a tree. It observes a serpent on the ground making an angle of depression of \[{30^\circ }\]. The peacock with the speed of \[300m{\min ^{ - 1}}\] catches the serpent in \[12\] seconds. What is the height of the tree ?

Answer 1

Hint: We have to find the height of the tree on the top of which the peacock is sitting. We solve this question using the concept of applications of trigonometry. We should also have the knowledge of the concept of the relation of the speed time and distance travelled by an object. We should also have the knowledge of the various trigonometric functions, we should have the knowledge of the values of trigonometric functions for various values of angles. First, we will construct the diagram for the given condition and then using the values of the trigonometric functions and the formula of speed and distance, we will find the height of the tree on which the peacock is sitting.

Complete step-by-step solution:
Given :
A peacock is sitting on the top of a tree. It observes a serpent on the ground making an angle of depression of \[{30^\circ }\]. The peacock with the speed of \[300m{\min ^{ - 1}}\] catches the serpent in \[12\] seconds.
Let us consider that the height of the tree is \[h\] m.
Construct : according to the question, we construct a diagram as shown

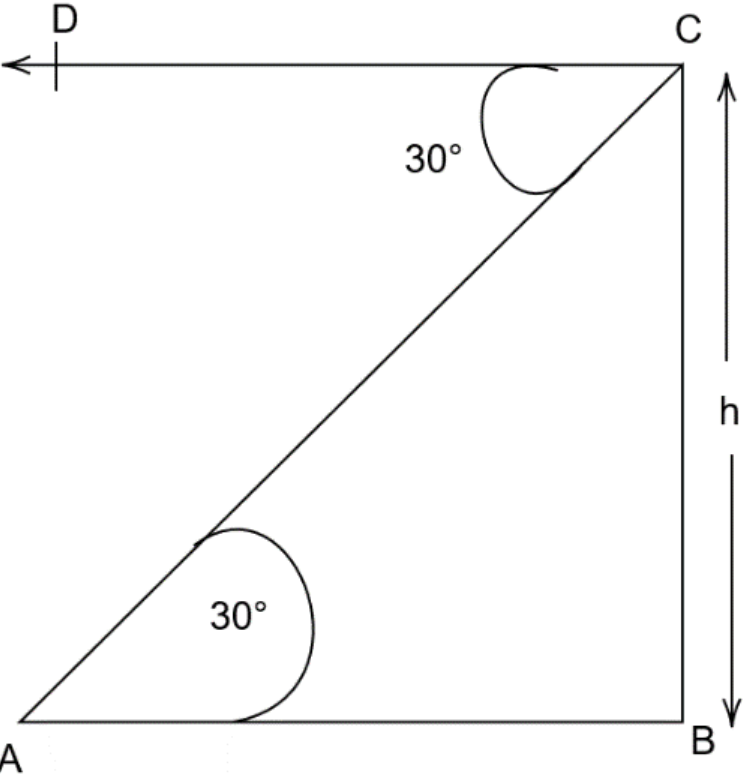
We are given that the angle of depression \[\angle DCA\] is \[{30^\circ }\].
Now, we also know that the alternative angles of two parallel lines are equal.
So, using this property of angles of parallel lines we get the value of \[\angle BAC\] as :
\[\angle BAC{\text{ }} = \angle DCA\]
\[\angle BCA = {30^\circ }\]
We also know that the relation of speed, distance and time is given as :
\[speed = \dfrac{{dis\tan ce}}{{time}}\]
Now, as the serpent is at a fixed point \[A\]. The peacock has to travel a distance of \[AC\] to catch the serpent. So, using the relation of speed, distance and time we will find the value of \[AC\].
As the given speed is in terms of minutes, we will change it into seconds as we are given the time of distance travelled in terms of seconds.
We will change the units of min into seconds using the relation of minutes and seconds.
We know that the relation of min and seconds is given as :
\[1min = 60sec\]
Now, using the relation we get the value of speed in seconds as :
\[speed = 300 \times \dfrac{1}{{60}}\]
\[speed = 5m{\sec ^{ - 1}}\]
Now, putting the values in the formula of speed, we get the value of distance \[AC\] as :
\[5 = \dfrac{{AC}}{{12}}\]
\[AC = 60m\]
Now, we also know that the value of sine function is given as :
\[\sin \theta = \dfrac{{perpendicular}}{{hypotenuse}}\]
Putting the values in the formula, we get the relation as :
\[\sin BAC = \dfrac{{BC}}{{AC}}\]
\[\sin {30^\circ } = \dfrac{h}{{60}}\]
Now, we also know that the value of \[\sin {30^\circ } = \dfrac{1}{2}\].
Using the value, we get the value of \[h\] as :
\[\dfrac{1}{2} = \dfrac{h}{{60}}\]
On solving, we get the value of \[h\] as :
\[h = 30m\]
Hence, the value of the height of the tree on which the peacock is sitting is \[30m\].

Note: Applications of trigonometry is the property or the concept of trigonometry which can be used in our daily life to either find the length or the angle of elevations of a body, building, the length of the formation of shadow of an object due to light. We can also compute the value or the measurement for the depth in the river of an object above it. This can also help us in finding the speed of an object moving in a direction which is seen by a person sitting on a height.