Question

A path of width 3.5 m runs around a semicircular grassy plot whose perimeter is 72 m. Find the area of the path (use $\pi =\dfrac{22}{7}$ )
A. 173 ${{m}^{2}}$
B. 173.25 ${{m}^{2}}$
C. 203 ${{m}^{2}}$
D. 203.25 ${{m}^{2}}$

Answer 1

Hint: Find the radius of the outer boundary of the path(semi-circle) by adding the radius of plot and width of path. Calculate area of outer semi-circle and inner semi-circle (plot). Area of semicircle $=\ \dfrac{\pi {{r}^{2}}}{2}$Perimeter of semi-circle \[=\ \pi r+2r\].Then taking difference of both outer and inner area of semi-circle(plot) ,we get required area of path.

Complete step-by-step answer:
Hence, we have a semicircular grassy plot with perimeter 72m and a plot with width 3.5m runs around the plot; so, we need to determine the area of the path.
Let the radius of the plot is ‘r’ meter. So, we can draw a sketch as

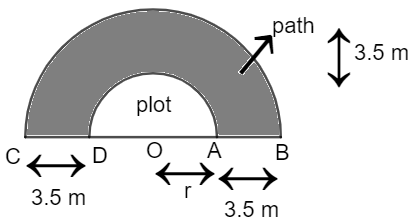
The plot is in the shape of the semi-circle and the path around it is of 3.5m width, so the outer boundary will form a semi-circle as well.
Now we can observe that the area of the path can be given by taking the difference of outer semi-circle (Arc CB) and inner semi-circle (Arc DA). So, we get,
Area of the path = (Area of semicircle with outer boundary of path - Area of semi-circle of plot or with inner boundary of path)
\[\Rightarrow \] Area of path = Area of semi-circle (Arc CB) - Area of semi-circle (Arc DA). ………………………….(i)
Now, we can calculate radius r of the plot with the help of the perimeter given in the question.
We know that perimeter is the total length of a continuous line forming the boundary of a closed geometric figure.
So, the perimeter of the semicircle is the sum of the length of the curvature part and diameter as well.
Circumference (curvature part) of the whole circle is given as \[2\pi r\], so, length of curve for semi-circle is \[\dfrac{2\pi r}{2}=\pi r\]
Perimeter of semi-circle (Arc DA) \[=\dfrac{2\pi r}{2}+2r\]
\[=\ \pi r+2r\]
Now, we know the perimeter of the given plot is 72m from the question. Hence, we get
\[\pi r+2r=72\]
Now, put \[\pi \ =\ \dfrac{22}{7}\], so, we get
\[\dfrac{22}{7}r+2r\ =\ 72\]
\[\dfrac{22r+14r}{7}=\ 72\]
\[\dfrac{36r}{7}=\ 72\]
\[\Rightarrow r=\dfrac{72\times 7}{36}=2\times 7=14m\]
So, radius ‘r’ of the semi-circle (Arc DA) (plot) is \[14\]m.
Now, we can get the radius of the semi-circle (Arc CB) by adding the length OA and AB i.e. radius of (Arc DA) and width of the path.
So, radius of semi-circle (Arc CB) is
\[R=r+3.5=14+3.5=17.5\]
Where \[\text{R}\] is the radius of a semicircle (Arc CB).
Now, we know the area of circle is \[\pi {{r}^{2}}\], so, area of semicircle is \[\dfrac{\pi {{r}^{2}}}{2}\]. Hence, we can get area of (Arc CB) and (Arc DA) and put it in equation (i), so we can write
Area of path \[=\] Area of semi-circle (Arc CB) - Area of semi-circle (Arc DA)
\[=\dfrac{\pi {{\text{R}}^{2}}}{2}\ -\ \dfrac{\pi {{r}^{2}}}{2}\]
\[=\ \dfrac{\pi }{2}\left[ {{\text{R}}^{\text{2}}}-{{r}^{2}} \right]\]
\[\ =\dfrac{22}{2\times 7}\left[ {{\left( 17.5 \right)}^{\text{2}}}-{{\left( 14 \right)}^{2}} \right]\ \]
Now, use \[{{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)\] algebraic identity to simplify the above equation. So, we get
Area of path \[=\ \dfrac{22}{2\times 7}\left[ \left( 17.5-14 \right)\left( 17.5+14 \right) \right]\]
\[=\ \dfrac{22}{2\times 7}3.5\times 31.5\]
\[=\dfrac{22\times 0.5\times 31.5}{2}\]
\[=11\times 0.5\times 31.5\]
Hence, Area of path \[=173.25{{m}^{2}}\]
So, option (B) is the correct answer.

Note: One may use the formula for the perimeter of a semi-circle as \[\pi r\] and not consider the Diameter with it. So, be careful while writing the perimeter of a semi-circle. It is given as \[\pi r+2r\] by using the fundamental definition of perimeter i.e. perimeter is the length of the path forming boundary of a closed geometric figure.
Area of a semicircle is half the area of a circle i.e. \[\dfrac{\pi {{r}^{2}}}{2}\], don’t get confuse here as well, writing the area of the path by taking difference of outer and inner semi-circle is the key point of the question.
One can calculate \[\left( {{17.5}^{2}}-{{14}^{2}} \right)\] without using the identity \[\left( {{a}^{2}}-{{b}^{2}} \right)\]. Applying the identity makes it easier and hence further calculation will get flexible.