Question

A path 1 m wide is built along the border and inside a square garden of side 30m. Find
(I) The area of the path
(II) The cost of planting grass in the remaining portion of the garden at the rate of $Rs\;40\;/\;m^2$

Answer 1

Hint: In the first part of the question find the area of the square garden and then subtract the area of the inner garden to the square garden to find the area of the 1 m wide path.
In the second part of the question multiply the area of the inner garden to the given cost of per meter square to find the total cost of planting grass.
The area of a square is given by the formula \[Area = {a^2}\], where \[a\] is the length of each side of a square.

Complete step by step answer:
Given the side of the square garden \[a = 30m\]

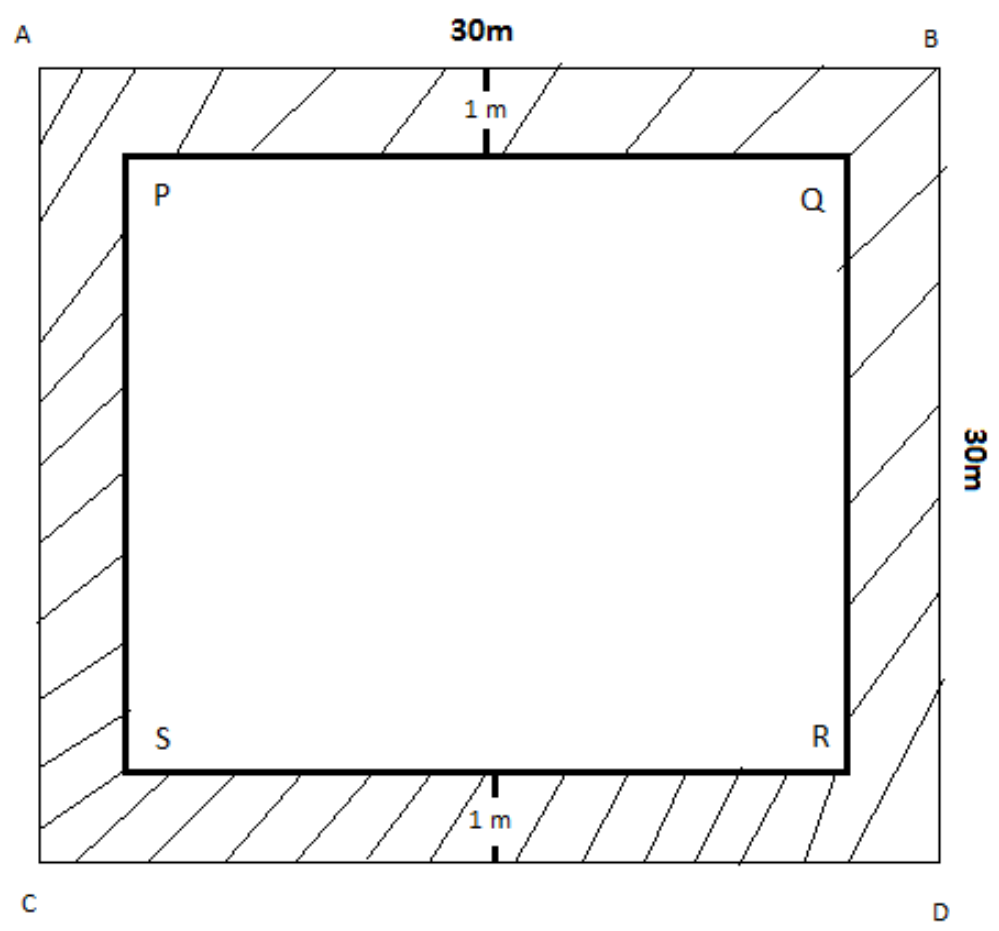
(I) From the figure we can see ABCD is the square garden and PQRS is the inner garden where the width of the path is 1m
 Since the width path of the path is 1m, so the length of the side \[PQ = AB - 1 - 1 = 30 - 1 - 1 = 28m\]
Also
\[PS = AC - 1 - 1 = 30 - 1 - 1 = 28m\]
Now from the length of the side PQ and PS we can say the inner part of the garden is also a square since it’s all sides are equal, so the area of the region PQRS will be
\[Are{a_{PQRS}} = 28 \times 28 = 784{m^2}\]
Now if we observe the diagram carefully we can say the area of the path will be the difference of the area of the garden and the area of the inner region hence we can say, the area of the path
 \[{Area_{path}} = {Area_{ABCD}} - {Area_{PQRS}}\]
Hence by substituting the values we get
\[Are{a_{path}} = \left( {30 \times 30} \right) - \left( {28 \times 28} \right) = 900 - 784 = 116{m^2}\]

(II) Since the area of the remaining portion of the garden PQRS\[ = 28 \times 28 = 784{m^2}\]
Hence the cost of planting grass in the remaining portion of the garden at the rate of $Rs\;40\;/\;m^2$ will be \[ = 784 \times 40 = Rs31360\]
So the cost of planting grass will be \[ = Rs\;31360\]

Note: Another method to find the area of the path is by finding the area of path for each side of the square path and then adding them up.
For the side AC and BD the area of the 1m wide path whose length is 30m will be \[ = 30 \times 1 + 30 \times 1 = 60{m^2}\].
For the side AB and CD the area of the 1m wide path whose length is 28m since \[PQ = 28m\] and \[PS = 28m\] will be \[ = 28 \times 1 + 28 \times 1 = 56{m^2}\].
So the area of the path will be \[ = 60 + 56 = 116{m^2}\].