Question

A password consists of two letters of the alphabet followed by three digits chosen from 0 to 9. Repeats are allowed. How many different possible passwords are allowed?
A.492804
B.650000
C.676000
D.1757600

Answer 1

Hint:
When the number of objects is “n”, and we have “r” ways for the selection of objects, then choosing an object can be in n different ways each time. Thus the permutation of objects when repetition is allowed will be equal to
$n \times n \times n \times \ldots \left( {r{\text{ }}times} \right) = {n^r}$
This question is solved with the help of multiplication principle, which states that if an event can occur in m different ways, following another event which can occur in n different ways, then the total number of occurrence of the events in the given order is .$m \times n$..
The above principle can be generalised for any finite number of events.
Required number of passwords = number of ways filling two places by using 26 letters, with repetition and remaining 3 places by using 0 to 9 digits when repetition is allowed i.e. by each with 10 ways.

Complete step by step solution:
We have to fill two places by alphabets and three places by digits and repetition is allowed.

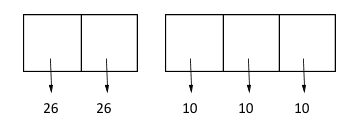
∴ First place can be filled by any of 26 letters and second place by same and at remaining each place can be filled by 10 ways.
∴ Total number of passwords = number of ways filling these five places
$\begin{gathered}
   = 26 \times 26 \times 10 \times 10 \times 10 \\
   = 676000 \\
\end{gathered} $
∴ Option (C) is correct.

Note:
A permutation is an act of arranging the objects or numbers in order. Combinations are the way of selecting the objects or numbers from a group of objects or collection, in such a way that the order of the objects does not matter.
The formula for permutations is: ${}^n{P_r} = \dfrac{{\left| \!{\underline {\,
  n \,}} \right. }}{{\left| \!{\underline {\,
  {n - r} \,}} \right. }}$