
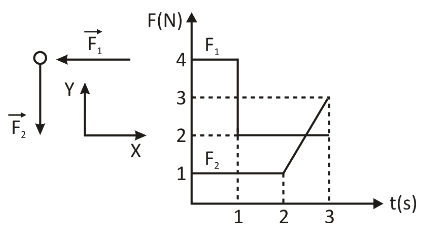
A particle with a mass of \[1\,{\text{kg}}\] is having a velocity of \[10\,{\text{m}}{{\text{s}}^{ - 1}}\] in the \[ + ve\] \[x - \] direction at \[t = 0\] . Forces \[{\vec F_1}\] and \[{\vec F_2}\] act on the particle whose magnitudes are changing with time according to the variation shown in the figure. The magnitude of the velocity of the particle at \[t = 3\,{\text{s}}\] (neglect gravity effect) is found to be \[n\sqrt 5 \,{\text{m}}{{\text{s}}^{ - 1}}\] . Find the value of \[n\].
A. \[5\]
B. \[2\]
C. \[1\]
D. \[6\]

Answer
567.6k+ views
Hint: First of all, we will calculate the impulse along the \[x - \] direction and the \[y - \] direction. From this step we will calculate the horizontal and the vertical component of the velocity. After that we will find the resultant velocity by manipulating accordingly. We will compare the velocity given in the question with the velocity that we will find to find the value of \[n\] .
Complete step by step solution:
In the given question, we are supplied the following data:
The mass of the particle is given as \[1\,{\text{kg}}\] .The velocity with which it is moving is given as \[10\,{\text{m}}{{\text{s}}^{ - 1}}\] . It is moving in the positive direction of the \[x - \] axis.There are two forces which act on the particle which are given as \[{\vec F_1}\] and \[{\vec F_2}\] . The magnitudes of the two forces are changing with time.The magnitude of the velocity of the particle at \[t = 3\,{\text{s}}\] (neglect gravity effect) is found to be \[n\sqrt 5 \,{\text{m}}{{\text{s}}^{ - 1}}\] .We are asked to find the value of \[n\] .
To begin with, we will try to find the both the horizontal component and the vertical component of the velocity. Before that we will find the impulse.We know, impulse defines the change in momentum of a body.Let us proceed to solve the numerical.
\[m = 10\,{\text{kg}}\]
\[\Rightarrow u = 10\hat i\]
For this we will draw the diagram, which is given below:
Impulse in the negative \[x - \] direction which is given by the area of the \[{F_1} - t\] graph.
$J = 4 \times 1 + 2 \times 2 \\
\Rightarrow J = 4 + 4 \\
\Rightarrow J = 8\,{\text{kg}}\,{\text{m}}{{\text{s}}^{ - 1}}$
Impulse is defined as the change in momentum.
So, we can write the expression of impulse as follows:
\[J = mv - mu\] …… (1)
Where,
\[J\] indicates the impulse.
\[m\] indicates the mass of the body.
\[v\] indicates the final velocity precisely the horizontal component of the velocity.
\[u\] indicates the initial velocity.
So, we will substitute the required values in the equation (1) and we get:
$J = mv - mu \\
\Rightarrow - 8 = 1 \times {v_{\text{x}}} - 1 \times 10 \\
\Rightarrow - 8 = {v_{\text{x}}} - 10 \\
\Rightarrow {v_{\text{x}}} = 2\,{\text{m}}{{\text{s}}^{ - 1}}$
Therefore, the horizontal component of the velocity is found to be \[2\,{\text{m}}{{\text{s}}^{ - 1}}\] .
Impulse in the \[y - \] direction which is given by the area of the \[{F_2} - t\] graph.
$m{v_{\text{y}}} - m \times 0 = 1 \times 3 + \dfrac{1}{2} \times 2 \times 1 \\
\Rightarrow 1 \times {v_{\text{y}}} = 3 + 1 \\
\Rightarrow 1 \times {v_{\text{y}}} = 4\,{\text{m}}{{\text{s}}^{ - 1}} $
Therefore, the horizontal component of the velocity is found to be \[4\,{\text{m}}{{\text{s}}^{ - 1}}\] .
So, the resultant velocity can be calculated as follows:
$v = \sqrt {v_{\text{x}}^2 + v_{\text{y}}^2} \\
\Rightarrow v = \sqrt {{2^2} + {4^2}} \\
\Rightarrow v = \sqrt {4 + 16} \\
\Rightarrow v = \sqrt {20} \\
\Rightarrow v = \sqrt {4 \times 5} \\
\Rightarrow v = 2\sqrt {5\,} \,{\text{m}}{{\text{s}}^{ - 1}} $
The resultant velocity is found to be \[2\sqrt {5\,} \,{\text{m}}{{\text{s}}^{ - 1}}\] .
As we are given in the question that the magnitude of the velocity is found to be \[n\sqrt 5 \,{\text{m}}{{\text{s}}^{ - 1}}\]. We will compare the velocity given in the question with the velocity we found above.
$n\sqrt 5 = 2\sqrt {5\,} \\
\therefore n = 5 $
Hence, the value of \[n\] is found to be \[5\] .
The correct option is B.
Note:While solving this problem, we must remember that impulse we calculated is along the negative \[x - \] direction. Most of the students tend to make mistakes at this point. It is important to remember that the initial velocity along the vertical component is zero.
Complete step by step solution:
In the given question, we are supplied the following data:
The mass of the particle is given as \[1\,{\text{kg}}\] .The velocity with which it is moving is given as \[10\,{\text{m}}{{\text{s}}^{ - 1}}\] . It is moving in the positive direction of the \[x - \] axis.There are two forces which act on the particle which are given as \[{\vec F_1}\] and \[{\vec F_2}\] . The magnitudes of the two forces are changing with time.The magnitude of the velocity of the particle at \[t = 3\,{\text{s}}\] (neglect gravity effect) is found to be \[n\sqrt 5 \,{\text{m}}{{\text{s}}^{ - 1}}\] .We are asked to find the value of \[n\] .
To begin with, we will try to find the both the horizontal component and the vertical component of the velocity. Before that we will find the impulse.We know, impulse defines the change in momentum of a body.Let us proceed to solve the numerical.
\[m = 10\,{\text{kg}}\]
\[\Rightarrow u = 10\hat i\]
For this we will draw the diagram, which is given below:

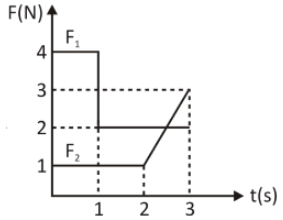
Impulse in the negative \[x - \] direction which is given by the area of the \[{F_1} - t\] graph.
$J = 4 \times 1 + 2 \times 2 \\
\Rightarrow J = 4 + 4 \\
\Rightarrow J = 8\,{\text{kg}}\,{\text{m}}{{\text{s}}^{ - 1}}$
Impulse is defined as the change in momentum.
So, we can write the expression of impulse as follows:
\[J = mv - mu\] …… (1)
Where,
\[J\] indicates the impulse.
\[m\] indicates the mass of the body.
\[v\] indicates the final velocity precisely the horizontal component of the velocity.
\[u\] indicates the initial velocity.
So, we will substitute the required values in the equation (1) and we get:
$J = mv - mu \\
\Rightarrow - 8 = 1 \times {v_{\text{x}}} - 1 \times 10 \\
\Rightarrow - 8 = {v_{\text{x}}} - 10 \\
\Rightarrow {v_{\text{x}}} = 2\,{\text{m}}{{\text{s}}^{ - 1}}$
Therefore, the horizontal component of the velocity is found to be \[2\,{\text{m}}{{\text{s}}^{ - 1}}\] .
Impulse in the \[y - \] direction which is given by the area of the \[{F_2} - t\] graph.
$m{v_{\text{y}}} - m \times 0 = 1 \times 3 + \dfrac{1}{2} \times 2 \times 1 \\
\Rightarrow 1 \times {v_{\text{y}}} = 3 + 1 \\
\Rightarrow 1 \times {v_{\text{y}}} = 4\,{\text{m}}{{\text{s}}^{ - 1}} $
Therefore, the horizontal component of the velocity is found to be \[4\,{\text{m}}{{\text{s}}^{ - 1}}\] .
So, the resultant velocity can be calculated as follows:
$v = \sqrt {v_{\text{x}}^2 + v_{\text{y}}^2} \\
\Rightarrow v = \sqrt {{2^2} + {4^2}} \\
\Rightarrow v = \sqrt {4 + 16} \\
\Rightarrow v = \sqrt {20} \\
\Rightarrow v = \sqrt {4 \times 5} \\
\Rightarrow v = 2\sqrt {5\,} \,{\text{m}}{{\text{s}}^{ - 1}} $
The resultant velocity is found to be \[2\sqrt {5\,} \,{\text{m}}{{\text{s}}^{ - 1}}\] .
As we are given in the question that the magnitude of the velocity is found to be \[n\sqrt 5 \,{\text{m}}{{\text{s}}^{ - 1}}\]. We will compare the velocity given in the question with the velocity we found above.
$n\sqrt 5 = 2\sqrt {5\,} \\
\therefore n = 5 $
Hence, the value of \[n\] is found to be \[5\] .
The correct option is B.
Note:While solving this problem, we must remember that impulse we calculated is along the negative \[x - \] direction. Most of the students tend to make mistakes at this point. It is important to remember that the initial velocity along the vertical component is zero.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




