Question

A particle (tied to a light string) is just able to complete a vertical circle of radius R. The speed of particle at P will be

Answer 1

Hint: For the particle to just complete a vertical circle, its velocity at the bottom most point must be equal to $v=\sqrt{5gR}$, where g is the acceleration due to gravity and R is the radius of the circle. Then use the work energy theorem to find the speed of the particle at point P.

Complete step by step answer:
It is given that a particle is tied to a light string. It is said that the particle is just able to complete a vertical circle of radius R. For the particle to just complete a vertical circle, its velocity at the bottom most point must be equal to $v=\sqrt{5gR}$, where g is the acceleration due to gravity and R is the radius of the circle.Let us say that the particle from the position of the bottom most point travels till P.

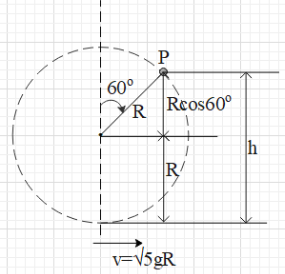
From the figure, we see that the particle goes up by a height of $h=R+R\cos {{60}^{\circ }}=R+R\left( \dfrac{1}{2} \right)=R\left( \dfrac{3}{2} \right)$.
When the particle goes up, the gravitational force does a negative work on the body which is equal to $W=-mgh$, where m is the mass of the particle.Form work energy theorem, we know that the work done on a particle is equal to change in its kinetic energy.
i.e. $W=\Delta K$.
The kinetic energy of a particle of mass m, moving with speed v is equal to $K=\dfrac{1}{2}m{{v}^{2}}$.
We know that the speed of the particle at the bottom most point is $v=\sqrt{5gR}$.
Therefore, its initial kinetic energy is equal to ${{K}_{i}}=\dfrac{1}{2}m{{\left( \sqrt{5gR} \right)}^{2}}$.
Let the velocity of the particle at point P be v. This means that its kinetic energy at that point is ${{K}_{f}}=\dfrac{1}{2}m{{v}^{2}}$.
Therefore, the change in kinetic energy of the particle is $\Rightarrow \Delta K={{K}_{f}}-{{K}_{i}}=\dfrac{1}{2}m{{v}^{2}}-\dfrac{1}{2}m{{\left( \sqrt{5gR} \right)}^{2}}$.
But we know that $W=\Delta K$.
$\Rightarrow mgh=\dfrac{1}{2}m{{v}^{2}}-\dfrac{1}{2}m{{\left( \sqrt{5gR} \right)}^{2}}$
$\Rightarrow 2gh={{v}^{2}}-5gR$
Substitute the value of h.
$\Rightarrow 2gR\left( \dfrac{3}{2} \right)={{v}^{2}}-5gR$
$\Rightarrow {{v}^{2}}=5gR+3gR$
$\Rightarrow {{v}^{2}}=8gR$
$\therefore v=\sqrt{8gR}$

Therefore, the speed of the particle at point P is equal to $\sqrt{8gR}$.

Note: The work done by the tension force in the string is zero because the direction of tension force is always perpendicular to the displacement of the particle. Gravity is a conservative force. When a conservative force acts on a particle, its mechanical energy remains constant. In other words, for conservative forces the mechanical energy of the system is conserved.