Question

A particle that is initially moving downwards towards the south in a vertically downward magnetic field is deflected towards the east. What is the sign of the charge on the particle?

Answer 1

Hint:Here one has to draw the x, y, z axis and the magnetic field lines along with the charge going downwards and then draw the charge going in the east direction. Here the charge experiences a magnetic force. Write the formula for force on a charge due to a magnetic field and solve in terms of vectors (i, j, and k).

Formula used:Force on a charge due to magnetic field.
$\overrightarrow F = q(\overrightarrow v \times \overrightarrow B )$
Here,
$\overrightarrow F $= Force;
$q$= Charge;
$\overrightarrow v $= Velocity;
$\overrightarrow B $= Magnetic Field;

Complete step by step solution:
The particle is moving downwards along the negative y direction.

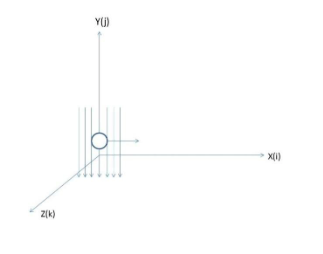
So,
$\overrightarrow v = v( - \overrightarrow j )$;
The magnetic field is also downwards
$\overrightarrow B = B( - \overrightarrow k )$;
Put the above two values in the equation given below
$\overrightarrow F = q(\overrightarrow v \times \overrightarrow B )$;
\[\overrightarrow F = q(\overrightarrow v ( - \overrightarrow j ) \times \overrightarrow B ( - \overrightarrow k ))\];
According to the vector identity (\[ - \overrightarrow j \times - \overrightarrow k = \overrightarrow i \]),
So,
\[\overrightarrow F = qvB\overrightarrow i \]
 Additional Information: There is another easy method of solving this question.
We can use Fleming’s Left hand rule;
We can see that the direction of the force is in the east while the particle and the magnetic field are acting in the downward direction. So,
$\overrightarrow F = q(\overrightarrow v \times \overrightarrow B )$; (Force on the particle)
$\overrightarrow F = qvb\sin \theta $;
Here the angle $\theta $is 90 degrees. So,
$\overrightarrow F = qvb\sin 90$ …($\sin 90 = 1$)
So, the equation becomes
$\overrightarrow F = qvb$;
In the above equation we can see that q is positive.
Final Answer: The equation (\[\overrightarrow F = qvB\overrightarrow i \]) means that if q has a positive sign then the force should act along the positive x axis, which is along the east and hence the sign change is positive.

Note: Draw the graph carefully; make sure to keep the direction of the magnetic field and the charge as it is mentioned in the question. Apply the sign and the properties of vectors carefully and put them in the given equation $\overrightarrow F = q(\overrightarrow v \times \overrightarrow B )$.