Question

A particle slides from rest from the topmost point of a vertical circle of radius (r) along a smooth chord making an angle ($$\theta $$) with the vertical. The time of descent is
A. least for $\theta = 0^\circ $
B. maximum for $\theta = 0^\circ $
C. least for $\theta = 45^\circ $
D. independent of $\theta $

Answer 1

Hint: First of all, we must draw the diagram to visualize the motion of the particle as it slides from rest from the topmost point of a vertical circle. Then using some trigonometry and equations of motion, we can find the time of descent of the particle.

Formula used:
The equations of motion are given as
$\eqalign{
  & v = u + at \cr
  & {v^2} - {u^2} = 2aS \cr
  & S = ut + \dfrac{1}{2}a{t^2} \cr} $
Here v and u are the final and initial velocities respectively, t is the time taken, a is the acceleration while S is the displacement.

Detailed step by step solution:

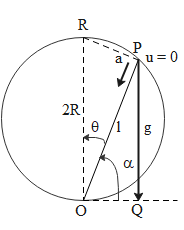
The above diagram shows a particle at point P. It is initially at rest and then allowed to move along the chord PO of the circle which has radius R. The acceleration of the particle is signified by ‘a’. The particle is moving at an angle $$\theta $$ with respect to the horizontal while the angle between the plane of motion of the particle and the horizontal is signified by $\alpha $. The acceleration of gravity is represented by g and is directed vertically downwards.
Now in $\Delta OPQ$, we can write the following expression
$a = g\sin \alpha = g\sin \left( {90^\circ - \theta } \right) = g\cos \theta $
Or we can also write in terms of various lengths that
$l = 2R\cos \theta $
Now we have the following equation of motion that we can apply for our case.
$S = ut + \dfrac{1}{2}a{t^2}$
We know that u = 0 and S = l, therefore, using other values we can write
$\eqalign{
  & l = \dfrac{1}{2} \times g\cos \theta \times {t^2} \cr
  & \Rightarrow 2R\cos \theta = \dfrac{1}{2} \times g\cos \theta \times {t^2} \cr
  & \Rightarrow t = 2\sqrt {\dfrac{R}{g}} \cr} $
This is the expression for time and we notice that in this expression, there is no dependence on the angle at which the particle moves downwards. This means that time of descent is the same for all angles or independent of the angle. The correct answer is option D.

Note: It should be noted that the expression $l = 2R\cos \theta $ is obtained by considering the right triangle ROP. Also we don’t go straight for topmost point R because we want to check the dependence on angle for the time of flight.