
A particle performs linear SHM of period 12 seconds and amplitude 8 cm. How long will the particle take to travel 6 cm from the extreme position?
A) 3.517 s
B) 2.517 s
C) 20.517 s
D) 8.517 s
Answer
584.7k+ views
Hint: The displacement of the particle can be given by the difference between the initial and final positions and as the particle is performing SHM, the expression for its displacement will be:
$x = A\cos \omega t$
and
$\omega = \dfrac{{2\pi }}{t}$ rad/sec
Using these, the time of required travel can be calculated
Complete step by step answer:
Given:
Time period (t) = 12 s
Amplitude (A) = 8 cm
Displacement (x) of the particle will be equal to the difference between the amplitude (A) and the distance to be travelled from the mean position:
x = (8 – 6) cm
x = 2 cm
Since, the particle is in simple harmonic motion its displacement from the positive extreme position is given as:
$x = A\cos \omega t$ ____________ (1)
We know,
$\omega = \dfrac{{2\pi }}{t}$ [As t = 12 s]
$\omega = \dfrac{\pi }{6}rad/s$
Substituting all the given values in (1), we get:
\[
x = A\cos \omega t \\
2 = 8\cos \left( {\dfrac{\pi }{6}t} \right) \\
\cos \left( {\dfrac{\pi }{6}t} \right) = 0.25 \\
\dfrac{\pi }{6}t = {\cos ^{ - 1}}0.25 \\
{\cos ^{ - 1}}0.25 \approx {75.52^ \circ } \\
\]
Converting radians into degree:
$75.52 \times \dfrac{\pi }{{180}}rad$
Now, calculating for t:
\[
\dfrac{\pi }{6}t = 75.52 \times \dfrac{\pi }{{180}} \\
t = \dfrac{{6 \times 75.52}}{{180}} \\
t = \dfrac{{75.52}}{{30}} \\
t = 2.517s \\
\\
\]
Therefore, the particle performing linear SHM will take 2.517 seconds to travel 6 cm from the extreme position and thus the correct option is B).
Note:Displacement refers to the difference between the final and initial positions of an object.
SHM is linear because it is always in a straight line and on a graph, it can be denoted as:
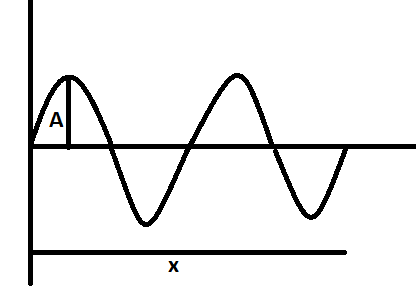
$x = A\cos \omega t$
and
$\omega = \dfrac{{2\pi }}{t}$ rad/sec
Using these, the time of required travel can be calculated
Complete step by step answer:
Given:
Time period (t) = 12 s
Amplitude (A) = 8 cm
Displacement (x) of the particle will be equal to the difference between the amplitude (A) and the distance to be travelled from the mean position:
x = (8 – 6) cm
x = 2 cm
Since, the particle is in simple harmonic motion its displacement from the positive extreme position is given as:
$x = A\cos \omega t$ ____________ (1)
We know,
$\omega = \dfrac{{2\pi }}{t}$ [As t = 12 s]
$\omega = \dfrac{\pi }{6}rad/s$
Substituting all the given values in (1), we get:
\[
x = A\cos \omega t \\
2 = 8\cos \left( {\dfrac{\pi }{6}t} \right) \\
\cos \left( {\dfrac{\pi }{6}t} \right) = 0.25 \\
\dfrac{\pi }{6}t = {\cos ^{ - 1}}0.25 \\
{\cos ^{ - 1}}0.25 \approx {75.52^ \circ } \\
\]
Converting radians into degree:
$75.52 \times \dfrac{\pi }{{180}}rad$
Now, calculating for t:
\[
\dfrac{\pi }{6}t = 75.52 \times \dfrac{\pi }{{180}} \\
t = \dfrac{{6 \times 75.52}}{{180}} \\
t = \dfrac{{75.52}}{{30}} \\
t = 2.517s \\
\\
\]
Therefore, the particle performing linear SHM will take 2.517 seconds to travel 6 cm from the extreme position and thus the correct option is B).
Note:Displacement refers to the difference between the final and initial positions of an object.
SHM is linear because it is always in a straight line and on a graph, it can be denoted as:

Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

10 examples of friction in our daily life




