Question

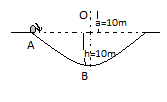
A particle of sass 20g is released with an initial velocity \[5{\text{ m/s}}\] along the curve from point A, as shown in the figure. The point A is at length h from B. The particle slides along the frictionless surface. When the particle reaches point B, its angular momentum O will be: (Take g=\[10{\text{ m}}{{\text{s}}^{ - 2}}\])

A) \[2{\text{ kg - }}{{\text{m}}^2}{{\text{s}}^{ - 1}}\]
B) \[8{\text{ kg - }}{{\text{m}}^2}{{\text{s}}^{ - 1}}\]
C) \[3{\text{ kg - }}{{\text{m}}^2}{{\text{s}}^{ - 1}}\]
D) \[6{\text{ kg - }}{{\text{m}}^2}{{\text{s}}^{ - 1}}\]

Answer 1

Hint: In this question, we need to determine the angular momentum of particle B when it reaches at point B. For this we will use the relation as \[\vec L = \vec r \times \vec p\], where
\[\vec L\] is the angular momentum of a moving particle about a point
\[\vec r\] is the length of perpendicular on the line of motion
\[\vec p\] is the component of momentum along the perpendicular to r

Complete step by step answer:
Mass of the particle \[m = 20g\]
The velocity of the particle at point a is \[{V_a} = 5{\text{ m/s}}\]
Since the velocity of the particle will be different for two points, hence we apply work-energy theorem from point A to B
\[{W_f} = \vartriangle KE - - (i)\]
For two points equation (i) can be written as
\[mgh = \dfrac{1}{2}mv_B^2 - \dfrac{1}{2}mv_A^2 - - (ii)\]
Equation (ii) can be further written as
\[
  mgh = \dfrac{1}{2}m\left( {v_B^2 - v_A^2} \right) \\
  2gh = v_B^2 - v_A^2 \\
 \]
Now by substitute the values of \[{v_A}\]and\[h\], we get
\[
  2gh = v_B^2 - v_A^2 \\
  \Rightarrow 2 \times 10 \times 10 = v_B^2 - {\left( 5 \right)^2} \\
  \Rightarrow v_B^2 - 25 = 200 \\
  \Rightarrow v_B^2 = 225 \\
  \Rightarrow {v_B} = 15{\text{ m/s}} \\
 \]
Hence the angular momentum about O will be
\[
  L = mv{r_{OB}} \\
   = \dfrac{{15}}{{1000}} \times 15 \times 20 \\
   = 6{\text{ kg - }}{{\text{m}}^2}{{\text{s}}^{ - 1}} \\
 \]
Option D is correct.

Note:Angular momentum is the same as linear momentum, but it is in rotational form. Angular momentum is a vector quantity, and it is the product of a body's rotational inertia and rotational velocity about a particular axis.