Question

A particle of mass m starts to slide down from the top of the fixed smooth sphere. What is the tangential acceleration when it breaks off the sphere?
A. $\dfrac{{2g}}{3}$
B. $\dfrac{{\sqrt 5 g}}{3}$
C. $g$
D. $\dfrac{{2g}}{3}$

Answer 1

Hint: One must remember basic forces acting on a particle when it is in circular motion. Besides this a well impactful thinking is required in order to understand the situation. Balancing the centripetal forces at the point of break off will provide a head start. Then applying energy conservation will link the situations and lead to results. Drawing diagrams will lend a helpful hand.

Complete step by step answer:

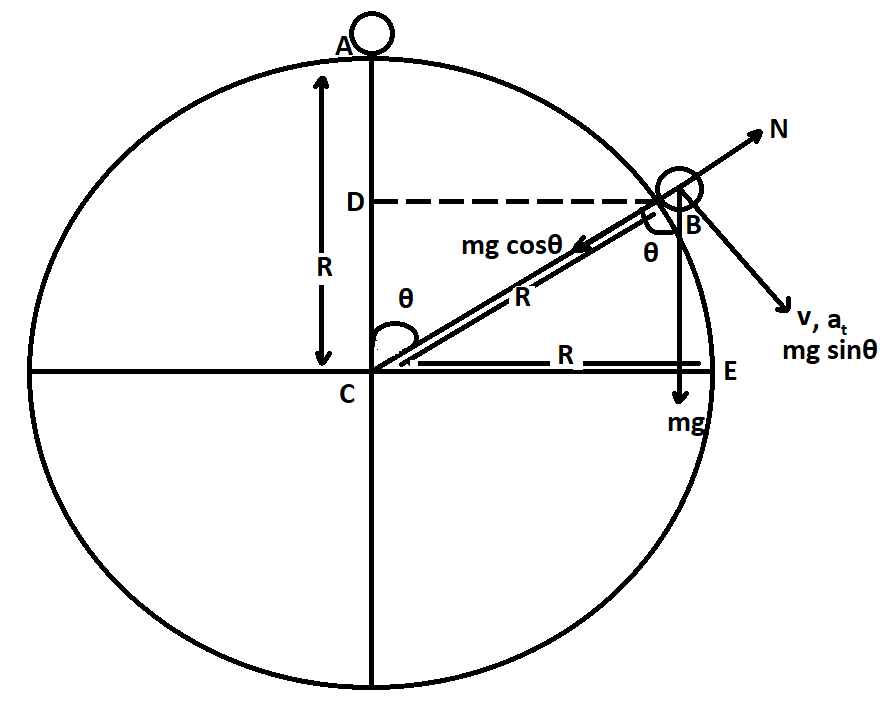
Let A be the initial position of the particle and B be the final position from where the particle loses contact.
Mass of particle is given m
Let velocity of particle at point of break off = v
Let radius of sphere = R
Forces acting on particle just before break off:
1. Downward gravitational force = mg
2. Centripetal force acting towards centre on sphere from that point = $\dfrac{{m{v^2}}}{R}$
3. Normal force = N
Angle between mg force and radius = $\theta $ ……… by alternate angles
Component of mg acting on centripetal force = $mg\cos \theta $
Equating forces acting along radius of sphere at point B
Centripetal Force + Normal Force = Component of mg acting on centripetal force
\[\;\dfrac{{m{v^2}}}{R} = mg\cos \theta + N\]
For particle to break off, normal force must be zero,
 \[\;\dfrac{{m{v^2}}}{R} = mg\cos \theta + 0\]
We can evaluate above equation as:
${v^2} = Rg\cos \theta $ …….. (i)
Now the particle starts from rest from point A and comes down to point B.
As A is the ground position of particles, so on descending to point B the particles have lost potential energy and gained kinetic energy.
Applying energy conservation:
Initial K.E. + Initial P.E. = Final K.E. = Final P.E.
$0 + 0 = \dfrac{1}{2}m{v^2} - mg\left( {AD} \right)$
$\dfrac{1}{2}m{v^2} = mg\left( {AD} \right)$ ……… (ii)
Where, AD = height descended by particles.
From figure it is evident that:
AC = Radius of sphere,
DC = $R\cos \theta $ and
AC – DC = AD
Putting values in above equation:
$R - R\cos \theta = AD$
Applying value of AD in equation (ii):
$\dfrac{1}{2}m{v^2} = mg\left( {R - R\cos \theta } \right)$
Equating above equation will yield:
${v^2} = 2Rg\left( {1 - \cos \theta } \right)$ ……….. (iii)
Both equations (i) and (iii) give value of ${v^2}$ , equating both equation
${v^2} = 2Rg\left( {1 - \cos \theta } \right) = Rg\cos \theta $
Evaluating above equation will give:
$\cos \theta = \dfrac{2}{3}$
According to trigonometry:
$\cos \theta = \dfrac{B}{H} = \dfrac{2}{3}$
$\sin \theta = \dfrac{P}{H}$
Where,
B = Base
H = Hypotenuse
Let perpendicular = P
Applying Pythagoras theorem:
${H^2} = {P^2} + {B^2}$
$P = \sqrt {{H^2} - {B^2}} = \sqrt {{{\left( 3 \right)}^2} - {{\left( 2 \right)}^2}} $
$P = \sqrt 5 $
If we look again into the sphere and particle, we know that tangential acceleration is acting in the direction of velocity of the particle. In the direction of velocity if we balance the forces we will notice only the presence of one force i.e. sin component of mg.
Let tangential acceleration = ${a_t}$
Applying Newton’s law of motion only in tangential direction of particle:
$Force = m{a_t} = mg\sin \theta $
Evaluating above equation will give
${a_t} = g\sin \theta $
Applying value of $\sin \theta $ will give,
${a_t} = \dfrac{{\sqrt 5 }}{3}g$
Tangential acceleration in the particle when it breaks off the sphere is $\dfrac{{\sqrt 5 }}{3}g$

Note: Centripetal force and Centrifugal force are the two forces that keep a particle maintain its circular motion. Centripetal force acts towards the centre of the circle and helps the particle follow the circular trajectory. Centrifugal force acts opposite to centripetal force i.e. outward force acting on particles in circular motion. In the given question there is no recital of centrifugal force because the particle is in contact with the surface of the sphere and the outward force it experiences is not due to its motion but due to normal force acting due to contact with the surface.