Question

A particle of mass $m$ moves with the potential energy $U$ as shown below. The period of the motion when the particle has total energy $E$ is:

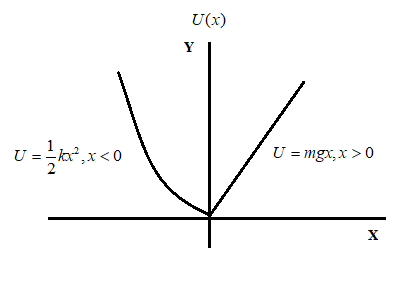
A. $2\pi\sqrt{\dfrac{m}{k}}+4\sqrt{\dfrac{2E}{mg^{2}}}$
B. $2\pi\sqrt{\dfrac{m}{k}}$
C. $\pi\sqrt{\dfrac{m}{k}}+2\sqrt{\dfrac{2E}{mg^{2}}}$
D. $2\sqrt{\dfrac{2E}{mg^{2}}}$

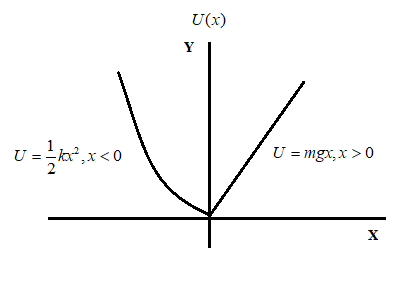
Answer 1

Hint: Here, we have a particle whose potential energy graph is given to us. From the graph we can see that the potential energy of the graph varies with respect to the negative and positive of the x axis. Thus to find the total energy, we must calculate the energy of the sides individually and then add them up.
Formula used:
$F=-\dfrac{dU}{dx}$

Complete answer:
 Let's assume that the time period of the motion be $T$ and the total energy be $E$.
Let us first look at the negative x-axis. Here the potential energy $U(x)=\dfrac{1}{2}kx^{2}$. Now the time taken by the particle is given as $T_{l}$
The force $F$ on the left side is given as $F=-\dfrac{dU}{dx}$
$\implies F=-\dfrac{2kx}{2}$
$\implies F=-kx$
We also know that $F=ma$
Then we have $ma=-kx$
$\implies a=-\dfrac{kx}{m}$
Clearly, the left side motion of the particle is SHM, since $a\propto (–x)$
Then comparing $a=-\omega^{2}x$ to the above equation, we get $\omega^{2}=\dfrac{k}{m}$
$\implies \omega=\sqrt{\dfrac{k}{m}}$
Since this occurs during time period $T$, we get,
$\implies \dfrac{2\pi}{T}=\sqrt{\dfrac{k}{m}}$
$\implies T=2\pi\sqrt{\dfrac{m}{k}}$
Since SHM is a to-and-fro motion, we can say that, $T_{l}=\dfrac{T}{2}=\pi\sqrt{\dfrac{m}{k}}$
Similarly, now consider the right side of the graph, we have $U(x)=mgx$
The force $F$ on the left side is given as $F=-\dfrac{dU}{dx}$
$\implies F=-mg$
$\implies a\propto –g$
If $u$ is the velocity of the particle, then the kinetic energy of the particle is given as $KE=\dfrac{1}{2}mu^2$
Then the total energy of the particle on the right side is given as $E=KE=\dfrac{1}{2}mu^2$
$\implies u=\sqrt{2E}{m}$
Then the time taken by the particle along the right side is given as $v’=u-gt$, when $v’$ is zero, we have ,
$\implies u=gt$
$\implies t=\dfrac{u}{g}$
$\implies t=\dfrac{\sqrt{2E}{m}}{g}$
Then, considering the to-and-fro motion $T_{r}=\dfrac{2\sqrt{2E}{m}}{g}$
Then the total time take $T$ is given as $T=T_{l}+T_{r}$
$\implies T=\pi\sqrt{\dfrac{m}{k}}+\dfrac{2\sqrt{2E}{m}}{g}$

Thus the correct answer is option C. $\pi\sqrt{\dfrac{m}{k}}+2\sqrt{\dfrac{2E}{mg^{2}}}$

Note:
To solve this sum we must note the following:
The left side and the negative side of the graph have different potential energy and hence different acceleration and time period. When considering the time period of any particular side, we must also account for the too and for motion of the particle.