Question

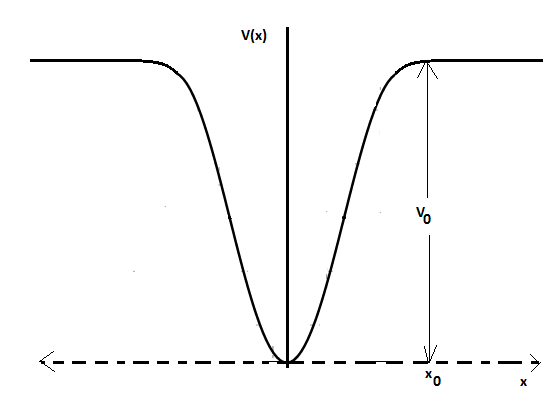
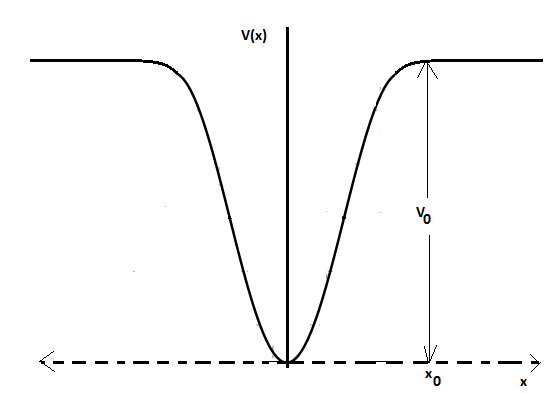
When a particle of mass \[m\] moves on the x-axis in a potential of the form \[V\left( x \right)=k{{x}^{2}}\], it performs simple harmonic motion. The corresponding time period is proportional to \[\sqrt{\dfrac{m}{k}}\], as can be seen easily using dimensional analysis. However, the motion of a particle can be periodic even when its potential energy increases on both sides of \[x=0\] in a way different from \[k{{x}^{2}}\] and its total energy is such that the particle does not escape to infinity. Consider a particle of mass \[m\] moving on the x-axis. Its potential energy is \[V\left( x \right)=\alpha {{x}^{4}}\] \[\left( \alpha >0 \right)\]for \[\left| x \right|\]near the origin and becomes a constant equal to \[{{V}_{0}}\] for \[\left| x \right|\ge {{x}_{0}}\] (see figure).
For periodic motion of small amplitude \[A\], the time period \[T\] of this particle is proportional to:

\[A)A\sqrt{\dfrac{m}{\alpha }}\]
\[B)\dfrac{1}{A}\sqrt{\dfrac{m}{\alpha }}\]
\[C)A\sqrt{\dfrac{\alpha }{m}}\]
\[D)A\sqrt{\dfrac{2\alpha }{m}}\]

Answer 1

Hint: Using dimensional analysis we can solve this question. Here, we have the same three variables in all four options, i.e., \[\text{A, }\!\!\alpha\!\!\text{ and m}\]. Find the dimension of each variable, and check options one by one to see which one has the same dimension as time period.
Formula used:
\[P.E=mgh\]

Complete step by step answer:

Using dimensional analysis, we can solve this question.
Dimension of time period, \[\left[ T \right]=\left[ {{M}^{0}}{{L}^{0}}{{T}^{1}} \right]\]
Now,
Let’s find out the dimension of \[\text{ }\!\!\alpha\!\!\text{ }\].
Given that,
\[V\left( x \right)=\alpha {{x}^{4}}\],\[\left( \alpha >0 \right)\] ---- 1
From equation 1, we get,
\[\alpha =\dfrac{V\left( x \right)}{{{x}^{4}}}\]
Here\[V\left( x \right)\]is potential energy and \[x\]indicates length.
Let’s find the dimensions of potential energy and length.
Potential energy, \[P.E=mgh\] -------1
Where,
\[m\] is the mass of the object
\[g\] is the acceleration due to gravity
\[h\] is the height
We have,
\[\left[ m \right]=\left[ {{M}^{1}} \right]\]
\[\left[ g \right]=\left[ {{M}^{0}}{{L}^{1}}{{T}^{2}} \right]\]
\[\left[ h \right]=\left[ {{L}^{1}} \right]\]
Substitute dimensions of \[\text{m,g and h}\] in equation 1. We get,
\[\left[ P.E \right]=\left[ {{M}^{1}} \right]\times \left[ {{M}^{0}}{{L}^{1}}{{T}^{2}} \right]\times \left[ {{L}^{1}} \right]=\left[ {{M}^{1}}{{L}^{2}}{{T}^{-2}} \right]\]
Dimension of length, \[{{\left[ x \right]}^{4}}={{\left[ {{M}^{0}}{{L}^{1}}{{T}^{0}} \right]}^{4}}=\left[ {{M}^{0}}{{L}^{4}}{{T}^{0}} \right]\]
Then,
\[\dfrac{V\left( x \right)}{{{x}^{4}}}=\dfrac{\left[ {{M}^{1}}{{L}^{2}}{{T}^{-2}} \right]}{\left[ {{M}^{0}}{{L}^{4}}{{T}^{0}} \right]}=\left[ {{M}^{1}}{{L}^{-2}}{{T}^{-2}} \right]\]
\[\left[ \alpha \right]=\left[ {{M}^{1}}{{L}^{-2}}{{T}^{-2}} \right]\]
Here, \[A\]is amplitude. Then, \[\left[ A \right]=\left[ {{L}^{1}} \right]\]
We have, \[\left[ m \right]=\left[ {{M}^{1}} \right]\]
Then, checking options we can see that the dimension of the equation in the third option has the same dimension as the time period.
\[\left[ \dfrac{1}{A}\sqrt{\dfrac{m}{\alpha }} \right]=\dfrac{1}{\left[ {{L}^{1}} \right]}\times \dfrac{{{\left( \left[ {{M}^{1}} \right] \right)}^{\dfrac{1}{2}}}}{{{\left( \left[ {{M}^{1}}{{L}^{-2}}{{T}^{-2}} \right] \right)}^{\dfrac{1}{2}}}}=\dfrac{\left[ {{M}^{\dfrac{1}{2}}}{{L}^{0}}{{T}^{0}} \right]}{\left[ {{M}^{\dfrac{1}{2}}}{{L}^{0}}{{T}^{-1}} \right]}=\left[ {{M}^{0}}{{L}^{0}}{{T}^{1}} \right]\]
\[\left[ T \right]=\left[ \dfrac{1}{A}\sqrt{\dfrac{m}{\alpha }} \right]=\left[ {{M}^{0}}{{L}^{0}}{{T}^{1}} \right]\]

So, the correct answer is “Option B”.

Note:
Dimensional analysis has many applications. It can be used to convert a physical quantity from one system to another. Also dimensional analysis can be used to check the correctness of a physical relation and to obtain relationships among various physical quantities involved.