Question

A particle of mass m moves along a line PC with velocity v, as shown in the figure above. What is the angular momentum of the particle about P?

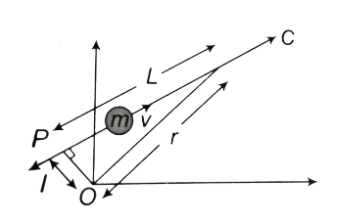
A. mvL
B. mvI
C. mvr
D. Zero

Answer 1

Hint: At first try to concentrate on the values that are given in the question and try to find the relationships between them. Now we have to write the general formula for angular momentum and then change it from vector form to scalar. Then we will have to figure out the angle between v and r. And then replace it in the main equation to get the required result.

Formula Used:
$\vec{L}=\vec{r}\times \left( m\vec{v} \right)$

Complete step-by-step answer:
In the question it says that there is a particle which has a mass ‘m’.
The particle is moving along a line that is PC.
The particle has a velocity v.
Now we are asked to find the angular momentum about point P.
Now, to solve this question we know that angular momentum vector can be represented by,
$\vec{L}=\vec{r}\times \left( m\vec{v} \right)$,
Now if we remove the vector sign then we can write the same thing as,
$L=rmv\sin \theta $

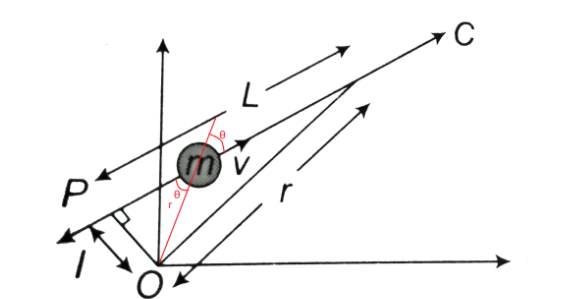
We can now figure out the angle between ‘r’ and ‘v’ from this diagram.
Now, we can say that $r\sin \theta =l$
So,
We already know that $L=mv\left( r\sin \theta \right)$.
So, on replacing this equation with $r\sin \theta =l$, we get,
$L=mvl$
which is actually written as,
$\text{angular momentum = linear momentum }\times \text{ lever arm}$
Therefore option B, mvl is the correct option.

Note: In the equation $L=rmv\sin \theta $, $\theta $ is the angle between r and v, m is the mass of the particle, r is actually the position vector of the particle and v is the velocity. Students must do all the substitution correctly to get the required answer, and must not do step jumping as each step contains marks.