Question

A particle of mass m is projected from the ground with an initial speed \[{{u}_{o}}\] at an angle \[\alpha \] with the horizontal. At the highest point of its trajectory, it makes a completely inelastic collision with another identical particle, which was thrown vertically upward from the ground with the same initial speed \[{{u}_{o}}\]. The angle that the composite system makes with horizontal immediately after collision is:
A. \[\dfrac{\pi }{4}\]
B. \[\dfrac{\pi }{4}+\alpha \]
C. \[\dfrac{\pi }{2}-\alpha \]
D. \[\dfrac{\pi }{2}\]

Answer 1

Hint: In this question, we are asked to calculate the angle made by the composite system of two particles. It is given that the two particles collide inelastically. Now, to solve this question we will need to conserve the momentum of both particles before and after the collision. As momentum is given by mass times velocity, we will therefore calculate the velocities of the particles during collision.
Formula Used: \[H=\dfrac{u_{o}^{2}{{\sin }^{2}}\alpha }{2g}\]
\[{{v}^{2}}={{u}^{2}}+2as\]

Complete answer:
It says that a particle with mass m is projected at angle and it collides inelastically with the other particle when it reaches the maximum height of the projectile as shown in the figure below.
          

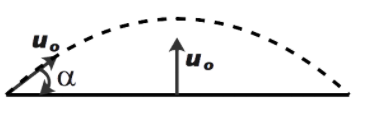
Now, we know that the distance travelled by particles projected upwards will be the maximum height of the projectile.
We know, height of the projectile is given by,
\[H=\dfrac{u_{o}^{2}{{\sin }^{2}}\alpha }{2g}\] …………. (1)
Now, using second kinematic equation to calculate the final velocity of the particle projected directly upward
We get,
\[{{v}^{2}}={{u}^{2}}+2as\]
Let’s say, \[{{v}_{2}}\] is the velocity of a particle before collision. Also, distance s is the height of the projectile
Therefore, from (1)
\[{{v}_{2}}^{2}={{u}_{o}}^{2}-2g\left( \dfrac{u_{o}^{2}{{\sin }^{2}}\alpha }{2g} \right)\]
On solving
We get,
\[{{v}_{2}}^{2}={{u}_{o}}^{2}(1-{{\sin }^{2}}\alpha )\]
Therefore,
\[{{v}_{2}}^{2}={{u}_{o}}^{2}{{\cos }^{2}}\alpha \]
Taking the square root
We get,
\[{{v}_{2}}={{u}_{o}}\cos \alpha \] ………….. (2)
We also know that at the highest point of projectile the particle will only have the velocity along X-direction, which is given by
\[{{v}_{1}}={{u}_{o}}\cos \alpha \] …………. (3)
Now, we know that the collision is inelastic therefore, the total mass of the system after collision will be 2m as shown in the figure. We know that final momentum must be equal to initial momentum in both X and Y direction. Let us say that velocity after collision is \[v'\].
            

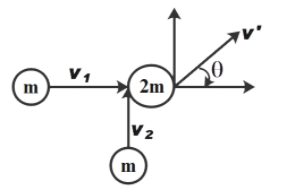
Therefore,
Now, conserving the momentum along X-direction
We can say
\[{{p}_{i}}={{p}_{f}}\]
Therefore,
\[m{{v}_{1}}+m{{v}_{2}}=2mv'\cos \theta \]
Now, we know that horizontal velocity of particles projected upwards will be zero and \[\theta \]is the angle with vertical after collision.
Therefore, we can write
\[{{u}_{o}}\cos \alpha =2v'\cos \theta \]
We can also say,
\[v'=\dfrac{{{u}_{o}}\cos \alpha }{2\cos \theta }\] ………………….. (4)
Now, conserving momentum along Y direction. We know that the velocity along Y direction of the first particle is zero i.e. \[{{v}_{1}}\] is zero
Therefore, we can write
\[m{{v}_{2}}=2mv'\sin \theta \]
After substituting values
We get,
\[{{u}_{o}}\cos \alpha =2v'\sin \theta \]
Therefore,
\[v'=\dfrac{{{u}_{o}}\cos \alpha }{2\sin \theta }\] ……….. ()
Now from (4) and (5)
We can say,
\[\dfrac{{{u}_{o}}\cos \alpha }{2\cos \theta }=\dfrac{{{u}_{o}}\cos \alpha }{2\sin \theta }\]
On solving
We get
\[\dfrac{\sin \theta }{\cos \theta }=1\]
Therefore,
\[\tan \theta =1\]
Now, we know
\[\tan \left( \dfrac{\pi }{4} \right)=1\]
Therefore,
\[\theta =\left( \dfrac{\pi }{4} \right)\]

Therefore, the correct answer is option A.

Note:
When two objects collide with each other inelastically, they stick to each other as a single mass. The mass of the system after inelastic collision is the total mass of the two objects before collision. The motion of the object projected at any particular angle is called the projectile motion.