Question

A particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be-
A. $qE{y^2}$
B. $q{E^2}y$
C. $qEy$
D. ${q^2}Ey$

Answer 1

Hint- Since the charged particle with charge q is in a uniform electric field E and the force applied on it will be F, the particle will move in the direction of the electric field with acceleration a. After a distance of y, the velocity of the particle at that point will be v.
Formula used: $K.E = \dfrac{1}{2}m{v^2}$, $F = Eq = ma$ and ${v^2} = {u^2} + 2as$.

Complete Step-by-Step solution:

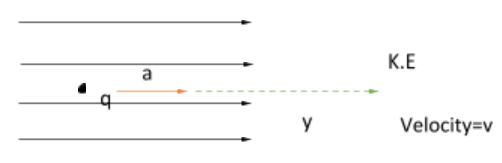
Now, we will find out the kinetic energy of the particle after moving a distance y.
The value of force will be-
Force = charge$ \times $electric field
Charge= q
Electric field= E
$ \Rightarrow F = qE$
Since we know that $F = ma$, we will put the value of F into the above equation, we get-
$
   \Rightarrow F = qE \\
    \\
   \Rightarrow ma = qE \\
    \\
   \Rightarrow a = \dfrac{{qE}}{m} \\
$
As we know that the third equation of motion is ${v^2} = {u^2} + 2as$, where u is initial velocity, v is final velocity and s is distance.
Since initial velocity is 0 as per the question, the value of v will be-
$ \Rightarrow {v^2} = 2as$
Putting the value of a and distance y into the above equation, we get-
$
   \Rightarrow {v^2} = 2as \\
    \\
   \Rightarrow {v^2} = 2\dfrac{{qE}}{m}y \\
$
The formula for kinetic energy is $\dfrac{1}{2}m{v^2}$. Substituting the value of ${v^2}$ into this, we have-
$
   \Rightarrow K.E = \dfrac{1}{2}m{v^2} \\
    \\
   \Rightarrow K.E = \dfrac{1}{2}m.2\dfrac{{qE}}{m}y \\
    \\
   \Rightarrow K.E = qEy \\
$
Thus, option C is the correct option.

Note: Kinetic energy, the type of energy that an object or a particle has by reason of its movement. In the event that work, which transfers energy, is done on a particle by applying a net force, the object accelerates and thus gains kinetic energy. Kinetic energy is a property of a moving object or particle and depends on its movement as well as on its mass.