Question

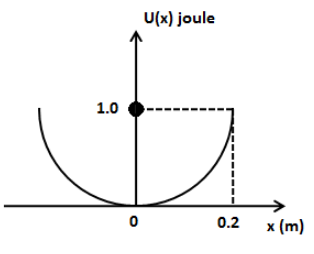
A particle of mass 4 kg moves simple harmonically such that its PE (U) varies with position x, as shown. The period of oscillation is

A. \[\dfrac{{2\pi }}{{25}}\,{\text{s}}\]
B. \[\dfrac{{\pi \sqrt 2 }}{5}\,{\text{s}}\]
C. \[\dfrac{{4\pi }}{5}\,{\text{s}}\]
D. \[\dfrac{{2\pi \sqrt 2 }}{5}\,{\text{s}}\]

Answer 1

Hint: Recall the formula for potential energy of the particle performing SHM. Then calculate the value of force constant from the potential energy of the particle. Use the formula for the period of the particle in SHM and substitute the value of mass and force constant.

Formula used:
Potential energy, \[U = \dfrac{1}{2}k{x^2}\]
Here, k is the force constant and x is the position of the particle from the mean position.
Period, \[T = 2\pi \sqrt {\dfrac{m}{k}} \]
Here, m is the mass of the particle.

Complete Step by Step Answer:
We have given that the mass of the particle performing harmonic motion is \[m = 4\,{\text{kg}}\], the potential energy of the particle is \[U = 1.0\,{\text{J}}\] and the position of the particle from the mean position is \[x = 0.2\,{\text{m}}\]. We can express the potential energy of the particle performing harmonic motion as,
\[U = \dfrac{1}{2}k{x^2}\]
Here, k is the force constant and x is the position of the particle from the mean position.
Rearranging the above equation for k, we get,
\[k = \dfrac{{2U}}{{{x^2}}}\]
Substituting \[U = 1.0\,{\text{J}}\] and \[x = 0.2\,{\text{m}}\] in the above equation, we get,
\[k = \dfrac{{2\left( 1 \right)}}{{{{\left( {0.2} \right)}^2}}}\]
\[ \Rightarrow k = 50\,{\text{N/m}}\]

We have the expression for the period of the particle performing harmonic motion,
\[T = 2\pi \sqrt {\dfrac{m}{k}} \]
Here, m is the mass of the particle.
Substituting \[m = 4\,{\text{kg}}\] and \[k = 50\,{\text{N/m}}\] in the above equation, we get,
\[T = 2\pi \sqrt {\dfrac{4}{{50}}} \]
\[ \Rightarrow T = 2\pi \sqrt {\dfrac{2}{{25}}} \]
\[ \therefore T = \dfrac{{2\pi \sqrt 2 }}{5}\,{\text{s}}\]

So, the correct answer is D.

Note:The period of particle in SHM is expressed as, \[T = \dfrac{{2\pi }}{\omega }\]. But since the angular frequency of the particle is \[\omega = \sqrt {\dfrac{k}{m}} \], the period becomes, \[T = 2\pi \sqrt {\dfrac{m}{k}} \]. Note that the mass should be in kilogram and the force constant k should be in N/m. Since both mass and force remain constant, the period remains the same in simple harmonic motion.