Question

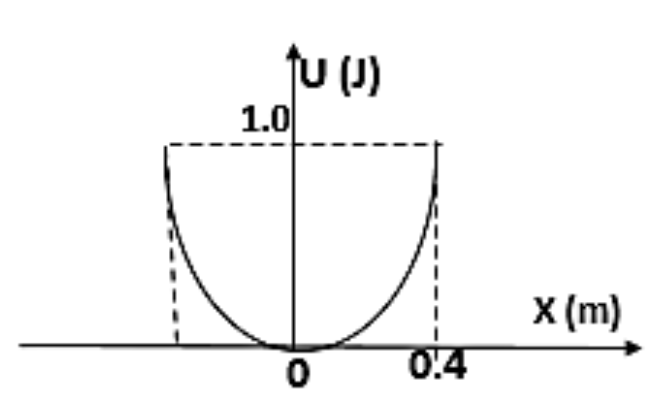
A particle of mass $2Kg$ moves in simple harmonic motion and its potential energy $U$ varies with position $X$ as shown. The period of oscillation of the particle will be:
 

$\begin{align}
  & A.\dfrac{2\pi }{5}s \\
 & B.\dfrac{2\sqrt{2}\pi }{5}s \\
 & C.\dfrac{\sqrt{2}\pi }{5}s \\
 & D.\dfrac{4\pi }{5}s \\
\end{align}$

Answer 1

Hint: Potential energy stored in a particle when it is in simple harmonic motion is given as,
$\dfrac{1}{2}k{{X}^{2}}=U$
And also the time period of oscillation can be written as,
$T=2\pi \sqrt{\dfrac{m}{k}}$
Where $m$ be the mass of the particle, $k$ be the spring constant and \[X\] be the height of the particle. First of all find the potential energy stored. From that find out the spring constant and calculate the time period.

Complete step by step answer:
the potential energy stored in a particle when it is undergoing a simple harmonic motion can be written as,
$\dfrac{1}{2}k{{X}^{2}}=U$
As per mentioned in the question,
Height of the particle is maximum so that we can write it as
$X=A$
Substituting these value in the energy equation will give rise to the spring constant of the particle,
That is,
$U=\dfrac{1}{2}k{{A}^{2}}=\dfrac{1}{2}\times k\times {{\left( 0.4 \right)}^{2}}=1$
By rearranging the equation,
$k=12.5N{{m}^{-1}}$
Now let us take a look at the time period of oscillation of the particle in the simple harmonic motion,
It can be written as,
$T=2\pi \sqrt{\dfrac{m}{k}}$
As per the question, it is already given that,
$m=2Kg$
And also, from the above calculations,
$k=12.5N{{m}^{-1}}$
Substituting these values in the equation will give,
$T=2\pi \sqrt{\dfrac{2}{12.5}}=\dfrac{4\pi }{5}s$

So, the correct answer is “Option D”.

Note: The spring constant is a number that indicates how much force it needs to stretch a substance. Particles with a higher spring constants are stiffer. Hooke's Law mentions that the force required to compress or extend a spring is proportional to the distance you elongate it.