Question

A particle of mass $2kg$ is on a smooth horizontal table and moves in a circular path of radius $0.6m$ . The height of the table from the ground is $0.8m$ . If the angular speed of the particle is \[12rad/s\], the magnitude of its angular momentum about a point on the ground right under the centre of the circle is:
(A) $14.4kg{m^2}{s^{ - 1}}$
(B) $11.52kg{m^2}{s^{ - 1}}$
(C) $20.16kg{m^2}{s^{ - 1}}$
(D) $8.64kg{m^2}{s^{ - 1}}$

Answer 1

Hint: We know that angular momentum of a body is the rotational equivalent of the linear momentum of the body. Just like linear momentum that remains conserved for any system, the angular momentum remains conserved for any closed system.
Mathematically angular momentum can be defined as the cross product of radius of circular motion and the linear momentum of the body.
$L = \overrightarrow r \times \overrightarrow p $ .
Formula used: We will be using the formula $\left| {\overrightarrow L } \right| = m\left| {\overrightarrow r } \right|\left| {\overrightarrow v } \right|\sin \theta $ where $\left| {\overrightarrow L } \right|$ is the magnitude of a vector quantity, the angular momentum of the body, $m$ is the mass of the body that undergoes angular momentum, $\left| {\overrightarrow r } \right|$ is the magnitude of the radius of the circular path of motion of the body, $\left| {\overrightarrow v } \right|$is the magnitude of another vector quantity, the velocity with which the body is travelling, and $\theta $ is the angle between the radius vector and the velocity vector.

Complete Step by Step answer:
We know that a body when it undergoes circular motion experiences velocity and momentum in a non-linear basis, this momentum and velocity the body experiences is called angular momentum and angular velocity. Angular momentum of a system is conserved and is related to the linear velocity of a body.
We know from the problem that the body of mass $m = 2kg$ is undergoing a circular motion along a path of radius $r = 0.6m$ which is about $h = 0.8m$ from a point on the ground. The body moves with an angular velocity of $\omega = 12rad/s$ .

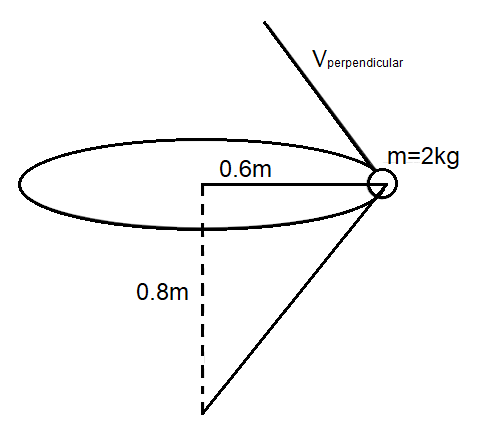
We know that angular momentum is the cross product of the radius vector and the linear momentum vector.
$L = \overrightarrow r \times \overrightarrow p $
We also know that the linear momentum is given by, $\overrightarrow p = mv$
Thus, calculating the angular momentum can be done using the formula,
$\left| {\overrightarrow L } \right| = m\left| {\overrightarrow r } \right|\left| {\overrightarrow v } \right|\sin \theta $ by substituting $\overrightarrow p = mv$
Now to find the resultant radius vector, we know that $\left| {\overrightarrow r } \right| = \sqrt {r_1^2 + r_2^2} $
$\left| {\overrightarrow r } \right| = \sqrt {{{\left( {0.6} \right)}^2} + {{\left( {0.8} \right)}^2}} $
$\left| {\overrightarrow r } \right| = \sqrt {0.36 + 0.64} = \sqrt {1.00} $
$ \Rightarrow \left| {\overrightarrow r } \right| = 1$
And the angle between the resultant radius vector and the linear velocity vector will be $\theta = 90^\circ $. Thus, angular momentum will be given by,
$\left| {\overrightarrow L } \right| = m\left| {\overrightarrow r } \right|\left| {\overrightarrow v } \right|\sin \theta $
$ \Rightarrow \left| {\overrightarrow L } \right| = 2 \times 1 \times \left| {\overrightarrow v } \right| \times \sin 90^\circ $
Anyways we know that the angular velocity in terms of linear velocity is given by, $v = \omega r$ . Substituting the values of $\omega = 12rad/s$ and $r = 0.6m$ we get,
$\left| {\overrightarrow L } \right| = 2 \times 1 \times 12 \times 0.6 \times \sin 90^\circ $ We know that $\sin 90^\circ = 1$ .
$\left| {\overrightarrow L } \right| = 2 \times 1 \times 12 \times 0.6 \times 1$
$\left| {\overrightarrow L } \right| = 14.4kg{m^2}{s^{ - 1}}$

Thus, the angular momentum of the system is $\left| {\overrightarrow L } \right| = 14.4kg{m^2}{s^{ - 1}}$ [option A]

Note: We can see that $\theta = 90^\circ $, this is because angular momentum when written in terms of linear momentum is a cross-product and hence considers only the perpendicular component of radius or motion.