Question

A particle of mass 1kg and carrying 0.01C is at rest on an inclined plane of angle ${{30}^{\circ }}$ with horizontal when an electric field of $\dfrac{490}{\sqrt{3}}N{{C}^{-1}}$ applied parallel to horizontal, the coefficient of friction is
$\begin{align}
  & \left( 1 \right)0.5 \\
 & \left( 2 \right)\dfrac{1}{\sqrt{3}} \\
 & \left( 3 \right)\dfrac{\sqrt{3}}{2} \\
 & \left( 4 \right)\dfrac{\sqrt{3}}{7} \\
\end{align}$

Answer 1

Hint: For a body inclined in a plane to come to rest, all forces acting on that object must balance with each other. For finding this, draw the free body diagram with the given data and mark all the forces that are acting on the body. Then by equating the forces we will get the coefficient of friction.

Formula used:
According to Newton’s second law,
F = ma = qE
where, F is the force
m is the mass
a is the acceleration
q is the charge
and E is the electric field

Complete step by step answer:
For a body inclined in a plane to come to rest, all forces acting on that object must balance with each other.

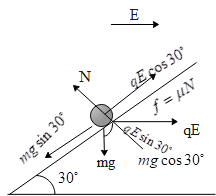
$\begin{align}
  & qE\cos \theta =\dfrac{490}{\sqrt{3}}\times 0.01\times \cos \theta \\
 & \Rightarrow qE\cos {{30}^{\circ }}=\dfrac{490}{\sqrt{3}}\times 0.01\times \dfrac{\sqrt{3}}{2} \\
\end{align}$
$\Rightarrow qE\cos {{30}^{\circ }}=2.45N$
$mg\sin \theta =1\times 9.8\times \sin {{30}^{\circ }}$
$\Rightarrow mg\sin \theta =1\times 9.8\times \dfrac{1}{2}=4.9N$
Therefore $qE\cos {{30}^{\circ }}\langle mg\sin {{30}^{\circ }}$
$N=mg\cos {{30}^{\circ }}+qE\sin {{30}^{\circ }}$
Substitute the value of m, g,q and E in the above equation we get,
$N=1\times 9.8\times \dfrac{\sqrt{3}}{2}+0.01\times \dfrac{490}{\sqrt{3}}\times \dfrac{1}{2}$
$N=4.9\sqrt{3}+\dfrac{4.9}{2\sqrt{3}}$
$\Rightarrow N=4.9\left( \sqrt{3}+\dfrac{1}{2\sqrt{3}} \right)$
$\Rightarrow N=9.9N$
$mg\sin \theta =1\times 9.8\times \sin {{30}^{\circ }}$$=f+qE\cos {{30}^{\circ }}$
Here, $f=\mu N$
Where, $\mu $ is the coefficient of friction.
Substitute in the above equation we get,
$\Rightarrow 4.9=\mu N+qE\cos {{30}^{\circ }}$
$\Rightarrow qE\cos {{30}^{\circ }}=2.45N$
$\Rightarrow \mu N=4.9-2.45$
$\mu =\dfrac{2.45}{N}$
$\begin{align}
  & \mu =\dfrac{2.45}{9.9} \\
 & \therefore \mu =0.0247=\dfrac{\sqrt{3}}{7} \\
\end{align}$
Therefore option (4) is correct.

Additional information:
Electric field can also be defined as the electric force acting per unit charge. The direction of the field is the same as the direction of the force. The electric field always goes out from a positive charge and always goes into a negative charge.

Note:
For a body inclined in a plane to come to rest, all forces acting on that object must balance with each other. Electric field can also be defined as the electric force acting per unit charge. The direction of the field is the same as the direction of the force. The electric field always goes out from a positive charge and always goes into a negative charge.