Question

A particle moving along a circular path of radius 6 meter with uniform speed of 8 meter per second. The average acceleration when the particle completes one half of the revolution is-
A. \[\dfrac{{16}}{{3\pi }}{\text{m/}}{{\text{s}}^2}\]
B. \[\dfrac{{32}}{{3\pi }}{\text{m/}}{{\text{s}}^2}\]
C. \[\dfrac{{64}}{{3\pi }}{\text{m/}}{{\text{s}}^2}\]
D. None of these

Answer 1

Hint: Particle has velocity tangential to the circle all the time when particle complete half of the circle then it changes its direction opposite to each other therefore initial velocity be $ - 8\mathop {\text{i}}\limits^ \wedge $ and final velocity be $8\mathop {\text{i}}\limits^ \wedge $.
Formula used:
${\text{Time}} = \dfrac{{{\text{distance}}}}{{{\text{speed}}}}$ and ${\text{Acceleration}} = \dfrac{{{\text{change in velocity}}}}{{{\text{total time taken}}}}$.

Complete step-by-step solution:

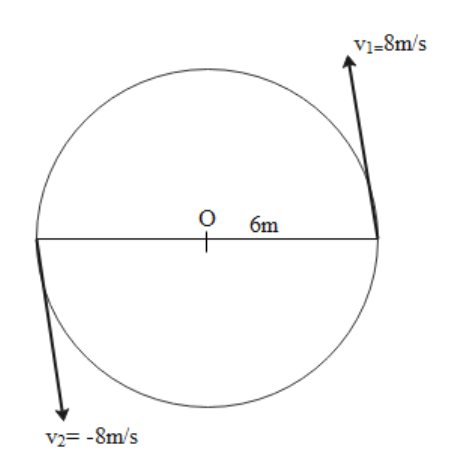
Given that,
Particle moves on a circular path with speed $ = 8{\text{m/s}}$
Radius of circular path i.e. ${\text{R = 6m}}$
We know that the particle has velocity tangential to the circle all the time when particle complete half of the circle than it change its direction opposite to each other,
Let the initial velocity be ${{\text{v}}_1}$ and final velocity be ${{\text{v}}_2}$
$\Rightarrow {{\text{v}}_1} = - 8\mathop {\text{i}}\limits^ \wedge $
 $\Rightarrow {{\text{v}}_2} = 8\mathop {\text{i}}\limits^ \wedge $
Particle completes one half revolution therefore distance travelled by particle is perimeter of circle divided by two $ = \dfrac{{2\pi {\text{R}}}}{2} = \pi {\text{R}}$
Therefore time taken $ = \dfrac{{{\text{distance}}}}{{{\text{speed}}}} = \dfrac{{\pi {\text{R}}}}{8} = \dfrac{{6\pi }}{8}{\text{sec}}$
And we know that acceleration $ = \dfrac{{{\text{change in velocity}}}}{{{\text{total time taken}}}}$
 $ = \dfrac{{{{\text{v}}_2} - {{\text{v}}_1}}}{{\text{t}}} \\
   = \dfrac{{8 - \left( { - 8} \right)}}{{\dfrac{{6\pi }}{8}}} \\
   = \dfrac{{64}}{{3\pi }}{\text{m/}}{{\text{s}}^2} \\ $
Hence the correct option is C.

Note: In this question, the particle moves on a circular path and completing one-half revolution therefore the distance traveled by the particle is one half of the perimeter of the circle and as speed is given so we calculated the time taken, after that, we applied the acceleration formula and the found the value of average acceleration to be $\dfrac{{64}}{{3\pi }}{\text{m/}}{{\text{s}}^2}$.