Question

A particle moves such that its acceleration is $ - by$ where $y$ is the displacement from equilibrium position and $b$ is a constant. If $A$ is its amplitude, the velocity of particle can be represented by
A. $\sqrt {\dfrac{{({A^2}{\text{ }} - {\text{ }}{y^2})}}{b}} \:$
B. $\sqrt {\dfrac{b}{{{A^2}{\text{ }} - {\text{ }}{y^2}}}} \:$
C. $\sqrt {b{\text{ }}({\text{ }}{A^2} - {\text{ }}{y^2})} \:$
D. \[b\sqrt {{A^2}{\text{ }} - {\text{ }}{y^2}} \]\:$

Answer 1

Hint: We will use a few identities of simple harmonic motion. We will compare the expressions for parameters in simple harmonic terms. Then we will try to evaluate the required parameter through the same proceedings.

Formulae used:
${a_o} = - {\omega ^2}y$
\[v = \omega r\]

Complete step by step answer:
Firstly, we are given with the expression for acceleration of the particle as
\[{a_o} = - by{\text{ }} - - - - - - - - - - - - - - - - - - - - - - - (i)\]
Also, given $A$ as the amplitude of the particle motion and $y$ as its arbitrary displacement.
Thus, if this is depicted diagrammatically, then we get a right angled triangle and we can say from our knowledge of geometry that the hypotenuse will be the amplitude $A$, the perpendicular will be the displacement $y$ and the base will be the radial element $r$.

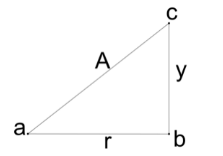
Thus, using the Pythagoras theorem, we can say the radial element of the particle motion can be calculated as
$r = \sqrt {{A^2} - {y^2}} {\text{ }} - - - - - - - - - - - - - - - - - - - - - - - (ii)$
Now, we also know that acceleration of a particle under simple harmonic motion is given by
${a_o} = - {\omega ^2}y{\text{ }} - - - - - - - - - - - - - - - - - - (iii)$
Thus, equating equations $(i)$ and $(iii)$, we get
$\omega = \sqrt b {\text{ }} - - - - - - - - - - - - - - - - - - - - (iv)$
Now, also, we know that
$v = \omega r{\text{ }} - - - - - - - - - - - - - - - - - - - - - - (v)$
Thus, substituting equations $(ii)$ and $(iv)$ in $(v)$, we get
$v = \sqrt b \times \sqrt {{A^2} - {y^2}} $
Multiplying further, we get
$\therefore v = \sqrt {b({A^2} - {y^2})} $

Thus, the correct answer is C.

Note: An alternative method to also solve this problem is by manipulating the given options through dimensional analysis. See, we are given with the expression of acceleration as,
\[{a_o} = - by\]
Now, clearly, $y$ has the dimension of length.
That means,
$[y] = [L]$
And the dimensions of acceleration can be written as
$[{a_o}] = [L{T^{ - 2}}]$
Thus, for dimensional consistency of the expression, ${\text{b}}$ should have its dimensions as
\[\left[ b \right] = \left[ {{T^{ - 2}}} \right]\]
And we are asked to find an expression of velocity having dimensions as
$[v] = \left[ {L{T^{ - 1}}} \right]$
Thus, the overall dimension of the final expression should be that of velocity. Now, in the first option, dimension is,
$\sqrt {\dfrac{{\left[ {{L^2}} \right]}}{{\left[ {{T^{ - 2}}} \right]}}} $
After further manipulation, we get the final dimension to be
$\sqrt {\left[ {{L^2}{T^2}} \right]} $
And finally we get
$\left[ {LT} \right]$
Which is clearly not the dimension for velocity. Then, we move to the second option.
The dimension of the expression is
$\sqrt {\dfrac{{[{T^{ - 2}}]}}{{\left[ {{L^2}} \right]}}} $
The final dimension comes out to be,
$[{L^{ - 1}}{T^{ - 1}}]$
Thus, this option also does not satisfy the dimensions of velocity.
Then, we go to the third expression having dimension
$\sqrt {[{T^{ - 2}}][{L^2}]} $
Thus, the final dimension turns out to be
$[L{T^{ - 1}}]$
Thus, this tallies with the dimension of velocity.Thus this is a correct option.
And the fourth expression having final dimensions of
$[L{T^{ - 2}}]$
Thus, it is not the correct option. Thus, dimensionally also the correct option is C. Students should be very cautious while manipulating the dimensions. It is recommended to use the first method which is a more generalized one than the alternative one which varies its feasibility question to question.