Question

A particle moves in the x-y plane with the velocity $\vec{v}=\hat{a}i+b\hat{x}j$ where a and b are constants. Initially, the particle was at the origin. The trajectory of the particle is.

Answer 1

Hint: First take out all the possible things that are given in the question, like the particles are in origin that is x=0, y=0, Then we have to find the equation of the trajectory which will reveal the type of graph then we need the radius of curvature to finalize the graph.

Complete step-by-step answer:
We can write a vector v in the form of,
$\vec{v}=\dfrac{dx}{dt}\hat{i}+\dfrac{dy}{dt}\hat{j}$
We know that the velocity of the particle is,
$\vec{v}=\hat{a}i+b\hat{x}j$,
So on comparing the equations on the upper hand we can say that,
$\dfrac{dx}{dt}=a$, and $\dfrac{dy}{dt}=bx$
We know, $\dfrac{dx}{dt}=a$
  $dx=adt$
 $\Rightarrow \int{dx=\int{adt}}$ (integrating on both sides)
$\Rightarrow x=at$ ……… Eq.1
We also know that, $\dfrac{dy}{dt}=bx$
 $\dfrac{dy}{dt}=bat$ ………(from Eq.1)
 $\Rightarrow dy=batdt$
 \[\Rightarrow \int{dy=\int{batdt}}\] (integrating on both sides)
Now,
 $y=\dfrac{1}{2}ab{{t}^{2}}$ ………Eq.2
On comparing Eq.1 and Eq.2, we get,
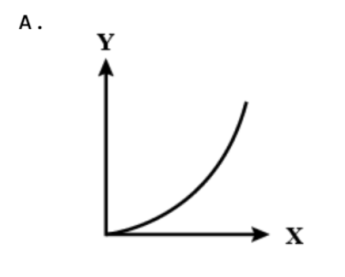
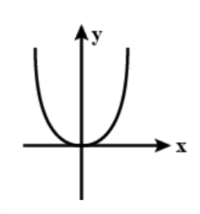
$y=\dfrac{b}{2a}{{x}^{2}}$ , This is the trajectory of the particle.
Answer is option (c)
 

Additional Information:
A curve is a line smooth in nature that does not take sharp turns to deviate; it deviates gradually resulting in an upward or downward curve.
A trajectory is the path that an object with mass in motion follows through space as a function of time. In classical mechanics, the mass might be a projectile or a satellite.
Origin is the starting point from which a body starts to move. It is generally taken as (0,0).
A graph usually depicts a body’s certain known values at a fixed time, using a graph we can derive the velocity, mass, acceleration, etc at point time. A curve is generally made to predict the pathway of a particle, not generally a particle but rockets, spaceships, planets and many other things also.


Note: Which equation results in what curve is a must know, students often make calculation mistakes, definition of origin. Y is taken as a function of x to get the equation of the curve. Compare the values with vector values properly, only then we can get the answer(dx/dt=a).