Question

A particle moves in east direction with $15m/\sec $ for $2\sec $ then moves in north direction with $5m/s$ for $8\sec $. Average velocity of the particle is:
(A). $1m/s$
 (B). $5m/s$
 (C). $7m/s$
 (D). $10m/s$

Answer 1

- Hint: You can start by describing what a vector quantity is. Then draw a well labelled diagram for the given problem with the resultant displacement vector. Then use the equation $Velocity = \dfrac{{Displacement}}{{Time}}$ to find out the distance traveled in east and north direction. Then use the Pythagoras theorem ( $A{C^2} = A{B^2} + B{C^2}$ ) to find out the net displacement. Then again use the equation $Velocity = \dfrac{{Displacement}}{{Time}}$ to calculate the result.

Complete step-by-step answer:
Before attempting the numerical calculations, let’s first discuss what a vector is?
A vector is a mathematical quantity that has both a magnitude (size) and a direction. To imagine what a vector is like, imagine asking someone for directions in an unknown area and they tell you, “Go $5km$ towards the West”. In this sentence, we see an example of a displacement vector, “ \[5km\] ” is the magnitude of the displacement vector and “towards the North” is the indicator of the direction of the displacement vector.
A vector quantity is different from a scalar quantity in the fact that a scalar quantity has only magnitude, but a vector quantity possesses both direction and magnitude. Unlike scalar quantities, vector quantities cannot undergo any mathematical operation, instead they undergo Dot product and Cross product.
Some examples of vectors are – Displacement, Force, Acceleration, Velocity, Momentum, etc.
The diagram of the movement of the particle is given below

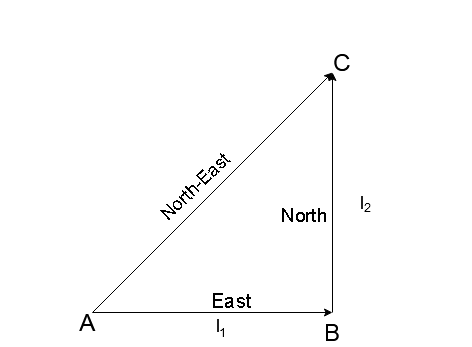
We know that
$Velocity = \dfrac{{Displacement}}{{Time}}$
The length of $AB$ is
$15 = \dfrac{{{l_1}}}{2}$
$ \Rightarrow {l_1} = 30m$
The length of $BC$ is
$5 = \dfrac{{{l_2}}}{8}$
$ \Rightarrow {l_2} = 40m$
By Pythagoras theorem
$A{C^2} = A{B^2} + B{C^2}$
$ \Rightarrow A{C^2} = {(30)^2} + {(40)^2}$
$ \Rightarrow A{C^2} = 900 + 1600$
$ \Rightarrow A{C^2} = 2500$
$ \Rightarrow AC = 50m$
Total time taken by the particle to get to point $C = 2 + 8 = 10\sec $ .
The average velocity of the particle is
$v = \dfrac{{50}}{{10}}$
$ \Rightarrow v = 5m/sec $
The average velocity of the particle is $5m/s$ in the north-east direction.
Hence, option B is the correct option.

Note: In this problem we are basically given three displacement vectors. The first two vectors $AB$ and $BC$ are mentioned in the given problem. The third vector $AC$ is the resultant vector which is used to reach the solution. In the diagram above, we arranged the vectors in a way that makes it easier to understand and solve.