Question

A particle moves in a circle of radius \[R = \dfrac{{21}}{{22}}{\text{m}}\] with a constant speed of 1m/s. Find, (a) magnitude of the average velocity and (b) magnitude of the average acceleration in 2s?

Answer 1

Hint:As, in the question the radius is given by which we can calculate the circumference, as the particle is moving 1m/s, so in 6s it can travel one complete circle.
The ${\text{Average}}\,{\text{velocity}} = \dfrac{{{\text{Total}}\,{\text{dispacement}}}}{{{\text{Total}}\,{\text{Time}}}}$ and the average acceleration is given by ${a_{av}} = \dfrac{{\left| {\Delta v} \right|}}{t}$ and here $\Delta v = {v_f} - {v_i} = \sqrt {{v^2} + {v^2} - 2vv\cos \theta } $.

Complete Step by Step Answer:

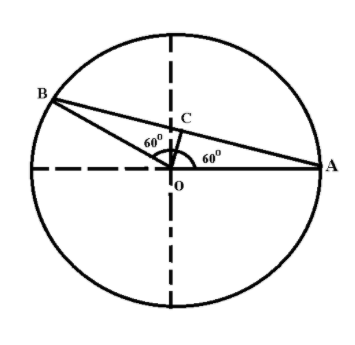
Given, the radius of the circle \[R = \dfrac{{21}}{{22}}{\text{m}}\] and particle is moving with a constant speed of 1m/s.
First find the circumference of the circle.
As, circumference of a circle is given by $2\pi R$, so use this formula to calculate its value.$C = 2\pi \left( {\dfrac{{21}}{{22}}} \right) = 2\left( {\dfrac{{21}}{7}} \right)\left( {\dfrac{{21}}{{22}}} \right) = 2\left( 3 \right) = 6{\text{m}}$.
So, the value of circumference will be 6m.
As, the speed of the particle is 1m/s, that is in 1 second it travels 1m , so this implies in 6 seconds it will travel 6m, i.e., one complete revolution (one complete circle).
So, in 6s it makes an angle of $360^\circ $.
In 1s it will make an angle of $60^\circ $.
Therefore, in 2s it will make an angle of $120^\circ $.
As, we need to find the average velocity in 2s, for that we need to find the total displacement in 2s.
Consider the above figure, let A be the initial point and B be the final point, after 2 seconds.
In $\Delta ABC$, $\angle AOB = 120^\circ $, $OA = OB = R$, let OC be the perpendicular on AB, such that $AC = BC$.
So, $\angle AOC = 60^\circ $.
It is clear that the displacement of the particle is AB, so we have to find its value, to find this value, consider the $\Delta AOC$,
$\sin 60^\circ = \dfrac{{AC}}{{AO}}$, here, AO is the radius and is equal to \[R = \dfrac{{21}}{{22}}{\text{m}}\].
So,
$
\sin 60^\circ = \dfrac{{AC}}{{\dfrac{{21}}{{22}}}} \\
AC = \dfrac{{21}}{{22}}\left( {\dfrac{{\sqrt 3 }}{2}} \right) \\
AC = \dfrac{{21\sqrt 3 }}{{44}} \\
 $
As, $AC = BC$, so $AC = BC = \dfrac{{21\sqrt 3 }}{{44}}$.
Now,
${\text{Average}}\,{\text{velocity}} = \dfrac{{{\text{Total}}\,{\text{displacement}}}}{{{\text{Total}}\,{\text{Time}}}}$
Total displacement is AB and total time taken is 2s. AB can be written as the sum of AC and BC. So, use these values and substitute in the formula.
$
{\text{Average}}\,{\text{velocity}} = \dfrac{{{\text{AC}} + {\text{BC}}}}{{\text{2}}} \\ {\text{Average}}\,{\text{velocity}} = \dfrac{{\dfrac{{21\sqrt 3 }}{{44}} + \dfrac{{21\sqrt 3 }}{{44}}}}{2} \\
  {\text{Average}}\,{\text{velocity}} = \dfrac{{21\sqrt 3 }}{{44}}\,{\text{m/s}} \\
 $
So, the magnitude of the average velocity in 2s is $\dfrac{{21\sqrt 3 }}{{44}}\,{\text{m/s}}$.
As, average acceleration is given by,
${a_{av}} = \dfrac{{\left| {\Delta v} \right|}}{t}$, here $\Delta v = {v_f} - {v_i}$, as, the angle between initial velocity and final velocity is $120^\circ $, therefore,
$
{v_f} - {v_i} = \sqrt {{v^2} + {v^2} - 2vv\cos 120^\circ } \\
\Rightarrow {v_f} - {v_i} = \sqrt {2{v^2} - 2{v^2}\left( { - \dfrac{1}{2}} \right)} \\
\Rightarrow {v_f} - {v_i} = \sqrt {2{v^2} + {v^2}} \\
\Rightarrow {v_f} - {v_i} = \sqrt {3{v^2}} \\
\Rightarrow {v_f} - {v_i} = \sqrt 3 v \\
\Rightarrow \Delta v = \sqrt 3 v \\
 $
Now, use this value to find the average acceleration,
${a_{av}} = \dfrac{{\left| {\Delta v} \right|}}{t} = \dfrac{{\sqrt 3 v}}{2}{\text{m/s}}$
So, the average acceleration of the particle will be $\dfrac{{\sqrt 3 v}}{2}{\text{m/s}}$.

Note:This is a question of kinematics, where the particle is moving in a circular path, it is given the particle is having a constant speed of 1m/s and by this we can get the in how much time the particle will complete one revolution. The, formula to calculate ${\text{Average}}\,{\text{velocity}} = \dfrac{{{\text{Total}}\,{\text{displacement}}}}{{{\text{Total}}\,{\text{Time}}}}$ and the average acceleration is given by ${a_{av}} = \dfrac{{\left| {\Delta v} \right|}}{t}$ and $\Delta v = {v_f} - {v_i} = \sqrt {{v^2} + {v^2} - 2vv\cos \theta } $.