Question

A particle moves in a circle of a radius of $2{\text{cm}}$ at a speed given by, $v = 4t$ where $v$ is in ${\text{cm}}{{\text{s}}^{ - 1}}$ and $t$ is in seconds. Find the total acceleration at $t = 1{\text{s}}$ .
A) $4\sqrt 5 {\text{cm}}{{\text{s}}^{ - 2}}$
B) $2\sqrt 5 {\text{cm}}{{\text{s}}^{ - 2}}$
C) $4\sqrt 3 {\text{cm}}{{\text{s}}^{ - 2}}$
D) $4{\text{cm}}{{\text{s}}^{ - 2}}$

Answer 1

Hint:The particle moving in the given circle will have a tangential acceleration and a centripetal acceleration. So the total acceleration of the particle will be the vector sum of these two accelerations. The tangential acceleration is given by the first derivative of the velocity of the particle.

Formulas used:
-The centripetal acceleration of a body is given by, ${a_c} = \dfrac{{{v^2}}}{r}$ where $v$ is the velocity of the body and $r$ is the radius of the circle.
-The tangential acceleration of a body moving in a circle is given by, ${a_t} = \dfrac{{dv}}{{dt}}$ where $v$ is the velocity of the body.

Complete step by step answer.
Step 1: List the parameters of the particle given in the question.

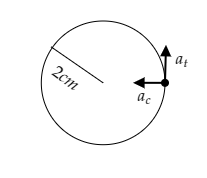
As seen in the above figure, the particle is moving in a circle and possesses a centripetal acceleration ${a_c}$ and a tangential acceleration ${a_t}$ .
The radius of the circle is given to be $r = 2{\text{cm}}$ .
The velocity of the particle is represented by $v = 4t$ where $t$ is the time.
We have to determine the total acceleration of the particle at $t = 1{\text{s}}$ .
The total acceleration ${a_T}$ is the vector sum of the tangential acceleration and the centripetal acceleration of the particle.
i.e., ${\vec a_T} = {\vec a_c} + {\vec a_t}$ --------- (1)
Step 2: Express the relation for the tangential acceleration of the particle to find its value at $t = 1{\text{s}}$ .
The tangential acceleration of the given particle moving in a circle is expressed as
${a_t} = \dfrac{{dv}}{{dt}}$ --------- (2)
Substituting for $v = 4t$ in equation (2) we get, ${a_t} = \dfrac{{d\left( {4t} \right)}}{{dt}} = 4$
So at $t = 1{\text{s}}$ , the tangential acceleration of the particle will be ${a_t} = 4{\text{cm}}{{\text{s}}^{ - 2}}$ .
Step 3: Express the relation for the centripetal acceleration of the particle to find its value at $t = 1{\text{s}}$ .
The centripetal acceleration of the given particle moving in a circle is expressed as
${a_c} = \dfrac{{{v^2}}}{r}$ --------- (3)
Substituting for $v = 4t$ and $r = 2{\text{cm}}$ in equation (3) we get, ${a_c} = \dfrac{{{{\left( {4t} \right)}^2}}}{2} = 8{t^2}$
So at $t = 1{\text{s}}$ , the centripetal acceleration of the particle will be ${a_c} = 8 \times {1^2} = 8{\text{cm}}{{\text{s}}^{ - 2}}$ .
Step 4: Express the total acceleration of the particle.
Equation (1) represents the total acceleration of the particle as ${\vec a_T} = {\vec a_c} + {\vec a_t}$ .
The magnitude of the total acceleration will be ${a_t} = \sqrt {{a_c}^2 + {a_t}^2} $ -------- (4)
Substituting for ${a_c} = 8{\text{cm}}{{\text{s}}^{ - 2}}$ and ${a_t} = 4{\text{cm}}{{\text{s}}^{ - 2}}$ in equation (4) we get,
${a_t} = \sqrt {{8^2} + {4^2}} = 4\sqrt 5 {\text{cm}}{{\text{s}}^{ - 2}}$
Thus the total acceleration of the particle is obtained as ${a_t} = 4\sqrt 5 {\text{cm}}{{\text{s}}^{ - 2}}$ .

So the correct option is A.

Note:The tangential acceleration of the particle is obtained to be ${a_t} = 4{\text{cm}}{{\text{s}}^{ - 2}}$ . This suggests that at any instant of time $t$ , the tangential acceleration will be constant. The tangential acceleration will be tangent at every point along the circle while the centripetal acceleration will be directed radially inwards as the centripetal force is what keeps the particle moving in the circle. The magnitude of a vector is given by the formula $a = \sqrt {{a_x}^2 + {a_y}^2} $ where ${a_x}$ and ${a_y}$ are the x-component and y-component of the vector $a$ .