Question

A particle moves from A to P and from P to B, as shown in the figure. Find the path length and displacement.

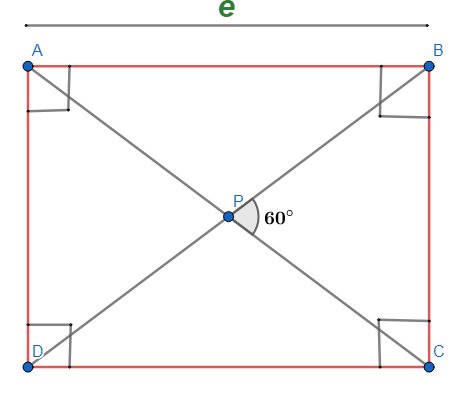
Answer 1

Hint: We need to determine the length AP and PB to answer this question. From the figure, it is clear that AP=PB. Also, we should know the distinction between path length and displacement.

Complete step by step answer:

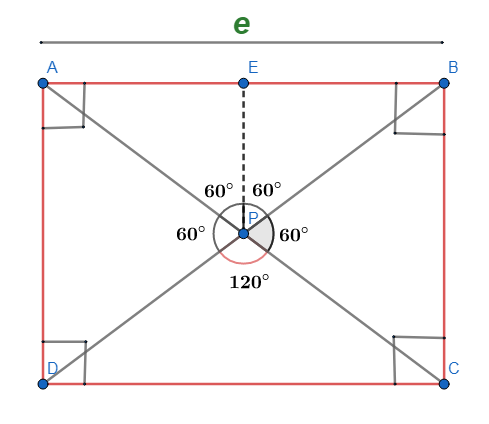
From the figure, we can see that the $\angle BPD=\angle APC={{60}^{\circ }}\text{ (VOA)}$ because they are vertically opposite angles. We also know that the sum of all the angles will be ${{360}^{\circ }}$. So the other two angles which are equal (vertically opposite angles), can be found out by,

 $\begin{align}
  & \angle BPD+\angle APC+\angle APB+\angle CPD={{360}^{\circ }} \\
 & {{60}^{\circ }}+{{60}^{\circ }}+2\angle APB={{360}^{\circ }} \\
\end{align}$

$\therefore \angle APB={{120}^{\circ }}$

After figuring out $\angle APB={{120}^{\circ }}$, we will drop a perpendicular from P to E on AB, which will divide AB into two equal parts AE and EB, which are equal sections of length $\dfrac{e}{2}$. The line PE splits the angle $\angle APB$ into two equal angles, i.e. $\angle APE=\angle BPE={{60}^{\circ }}$.

Considering the right triangle AEP, we can write

$\sin \left( {{60}^{\circ }} \right)=\dfrac{AE}{AP}=\dfrac{\left( \dfrac{e}{2} \right)}{AP}$
$AP=\dfrac{\left( \dfrac{e}{2} \right)}{\sin \left( {{60}^{\circ }} \right)}$
$\therefore AP=\dfrac{e}{\sqrt{3}}$

So, due to symmetry, PB will also be equal to $\dfrac{e}{\sqrt{3}}$.

So the path length is equal to the total distance travelled. So we can define path length as the sum of the lengths AP and PB,

$P.L=AP+PB$

$\text{P}\text{.L}=\dfrac{2e}{\sqrt{3}}$.

So the path length is the distance that the particle travelled from A to P and from P to B, which is equal to $\left( \text{P}\text{.L} \right)=\dfrac{2e}{\sqrt{3}}$.

But, the displacement will always be the shortest distance travelled; in this case, it will be the length of AB = e.

Note: In mechanics, displacement is a vector whose length is the shortest distance from the initial to the final position of a point P undergoing motion.
In mechanics, the Path length is the total distance travelled by the body from an initial point to a final point.