Question

A particle moves along the x axis with acceleration $a = 6(t - 1)$, where t is in seconds. If the particle is initially at the origin and moves along the positive x axis with ${v_o} = 2m/s$, analyze the motion of the particle.

Answer 1

Hint:Here to analyze the motion of a particle one has to know the particle velocity and time. Here we have to plot the graph for acceleration, velocity and displacement. We already know that acceleration is the rate change of velocity w.r.t time, velocity is the rate change of displacement w.r.t time. Integrate each variable i.e. a, v, d and plot the graph.

Complete step by step solution: Find out the velocity and the distance:

Acceleration is given as:

$a = 6(t - 1)$;
$ \Rightarrow $ $a = 6t - 6$;

Write acceleration in terms of velocity;

$\dfrac{{dv}}{{dt}} = 6t - 6$;

Take the time derivative on the RHS:

$\dfrac{{dv}}{{dt}} = 6t - 6$;
$ \Rightarrow $$dv = dt(6t - 6)$;

Integrate on both the sides:

$\int\limits_{{v_o}}^v v = \int\limits_0^t {(6t - 6)dt} $;

Put the limits and solve;

$v - {v_o} = \left[ {\dfrac{{6{t^2}}}{2} - 6t} \right]_0^t$;
$ \Rightarrow $$v - {v_o} = \dfrac{{6{t^2}}}{2} - 6t$;

The difference in velocity is:

$v - {v_o} = 3{t^2} - 6t$;

We have been given the initial velocity to be 2m/s:

$v - 2 = 3{t^2} - 6t$;
$ \Rightarrow $$v = 3{t^2} - 6t + 2$;

Now, we know that velocity is distance upon time so,

$\dfrac{{dx}}{{dt}} = 3{t^2} - 6t + 2$;
$ \Rightarrow $$\dfrac{{dx}}{{dt}} = 3{t^2} - 6t + 2$;

Take the time derivative to the RHS and integrate:

$dx = dt(3{t^2} - 6t + 2)$;

Integrate on the LHS from 0 to x and on the RHS from 0 to t.

$\int\limits_0^x {dx} = \int\limits_0^t {(3{t^2} - 6t + 2)dt} $;
$ \Rightarrow $$x = \int\limits_0^t {(3{t^2} - 6t + 2)dt} $;

Use integration by parts and solve;

\[x = \int\limits_0^t {(3{t^2}dt) + \int\limits_0^t { - 6tdt} + \int\limits_0^t {2dt} } \];

Take the constant out and solve:

$x = 3\int\limits_0^t {({t^2}dt) - 6\int\limits_0^t {tdt} + 2\int\limits_0^t {dt} } $;

Apply the theorem $\int {xdx = \dfrac{{{x^{n + 1}}}}{{n + 1}}} $;

$x = 3 \cdot \dfrac{{{t^3}}}{3} - \dfrac{{6{t^2}}}{2} + 2t$;
$ \Rightarrow $$x = 3 \cdot \dfrac{{{t^3}}}{3} - \dfrac{{6{t^2}}}{2} + 2t$;

Simplify the above equation
$x = {t^3} - 3{t^2} + 2t$;

Now, plot the graph for acceleration by putting t = 0 and then a = 0 in the below equation:

$a = 6t - 6$;

Put t = 0;

$ \Rightarrow $$a = - 6$;

Put a = 0;

$ \Rightarrow $$t = \dfrac{6}{6} = 1$;

Now, plot the graph:

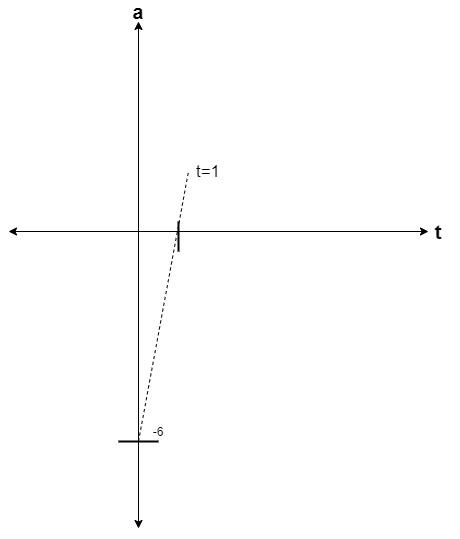
Now, similarly for velocity:

$v = 3{t^2} - 6t + 2$;

Take the common out;

$ \Rightarrow $$v = 3({t^2} - 2t) + 2$;

To make it ${(a - b)^2}$ subtract 3 from the above equation

$ \Rightarrow $$v = 3{(t - 1)^2} + 2 - 3$;
$v = 3{(t - 1)^2} - 1$;

Here${(t - 1)^2}$is equation for parabola, similar to $y = {x^2}$;

 Put x =1 and y = 0; So, the center lies at (1,0);

Plot the graph:
Here the minimum value of the velocity would be at t=-1;

$v = 3{(1 - 1)^2} - 1$;
$ \Rightarrow $$v = - 1$;

Similarly, Put t = 0;

$v = 3{(0 - 1)^2} - 1 = 2$;
The graph would be:

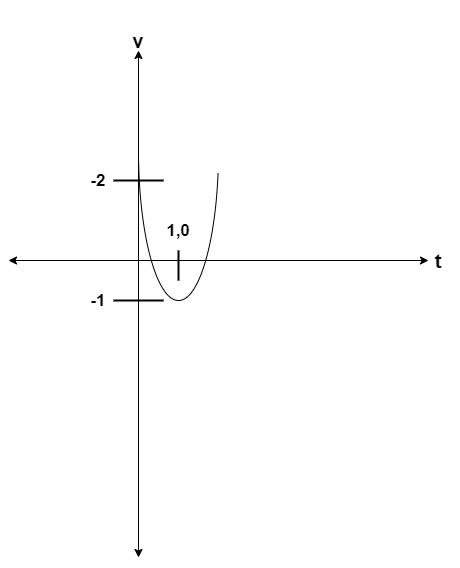
Similarly, for displacement x:

$x = {t^3} - 3{t^2} + 2t$;

Take the common out:

$x = t({t^2} - 3t + 2)$;

Factorize the above equation:

$x = t({t^2} - t - 2t + 2)$;

Take the common out:

$x = t(t(t - 1) - 2(t - 1))$;
$ \Rightarrow $$x = (t)(t - 2)(t - 1)$;

Now, equate each term to zero.

$t = 0;t - 2 = 0;t - 1 = 0$;
The value of t at which the displacement is zero would be
t = 0,1,2;
This means that the displacement of particles would be zero at 0 second, 1 second and 2 seconds.

Note:To know the momentum and position of the particle is impossible. Imagine a particle is moving with a speed of light, so the moment one tends to observe the particle at particular position at a particular time the speed of the particle is such that in the amount of time taken by the observer to observe the particle the particle would have changed its position, this is due to the fact that the particle is traveling at the speed of light. This phenomenon is known as the uncertainty principle.