Question

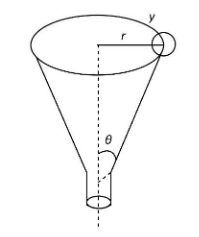
A particle is to slide along the horizontal circle on the inside of a conical funnel as shown. For the execution of this motion the velocity of the particle in terms of $r$ and $\theta $ in the Fig. is

A. $\sqrt {gr\tan \theta } $
B. $\sqrt {gr\cot \theta } $
C. $\sqrt {gr\sin \theta } $
D. $\sqrt {gr\cos \theta } $

Answer 1

Hint:We will first draw a free body diagram showing all the forces acting on the particle. We will balance all the vertical components of force and all the horizontal components of force acting on the particle and then derive an equation for the velocity of the particle.

Complete step by step answer:
Let $m$ be the mass of the particle, which is to slide along the horizontal circle of the funnel. Here, $r$ is the radius of the horizontal circle. We will first draw a diagram showing the forces acting on the particle.

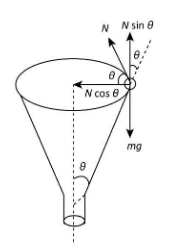
Let us write the equation for the force exerted on the particle by gravity as,
\[F = mg\]
Here, $g$ is the acceleration due to gravity.
Let $N$ be the normal reaction force on the particle lying at a point on the horizontal circle of the funnel. As seen from the diagram, the normal reaction force $N$ can be split into two components.The vertical component, which acts upwards ${N_y} = N\sin \theta $
The horizontal component, which acts towards the center ${N_x} = N\cos \theta $

From the diagram, we can see that the vertical component of $N$ equals the force of gravity. Hence, we write
$
{N_y} = mg\\
\Rightarrow N\sin \theta = mg\\
\Rightarrow N = \dfrac{{mg}}{{\sin \theta }}
$
Since the horizontal component of the normal force acts in the same direction as the centripetal force, both forces will be equal. Hence, we can write
$
\dfrac{{m{v^2}}}{r} = {N_x}\\
\Rightarrow\dfrac{{m{v^2}}}{r} = N\cos \theta
$
Here, $v$ is the velocity of the particle.
Now, we will insert the equation $N = \dfrac{{mg}}{{\sin \theta }}$ in the above equation to obtain a relation to find the velocity.
$
\dfrac{{m{v^2}}}{r} = \dfrac{{mg}}{{\sin \theta }} \times \cos \theta \\
\Rightarrow{v^2} = gr\dfrac{{\cos \theta }}{{\sin \theta }}\\
\Rightarrow {v^2} = gr\cot \theta \\
\therefore v = \sqrt {gr\cot \theta }
$
Hence, the equation for the velocity is obtained as $v = \sqrt {gr\cot \theta } $.

Therefore, option B is correct.

Note: It is to be noted that the normal reaction force acts tangential to the horizontal circle in which the particle moves. The horizontal component of this normal reaction force acting towards the centre provides the necessary centripetal force for keeping the particle in a circular motion. Therefore, the direction of acceleration of the particle is towards the centre and the particle slides through the funnel executing circular motion.