Question

A particle is projected from a point P (2, 0, 0) m with a velocity 10m/s making an angle 45º with the horizontal. The plane of projectile motion passes through a horizontal line PQ which makes an angle of 37º with positive x-axis, x-y plane is horizontal. The coordinates of the point where the particle will strike the line PQ is: (Take g = 10 m/s2)
(A) (10, 6, 0) m
(B) (8, 6, 0) m
(C) (10, 8, 0) m
(D) (6, 10, 0) m

Answer 1

Hint: The particle is projected from the ground making some angle with the horizontal. So, this is a problem of projectile motion. Also, a straight line is drawn PQ, making an angle with the horizontal and it starts from the point of projection of the particle. We need to find where the particle touches the line again. It touches the line at the ground at the point of projection.

Complete Step by step answer:

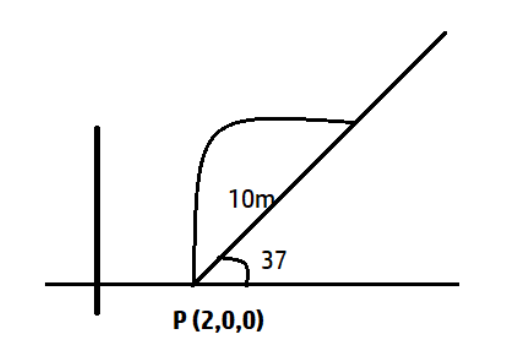
The particle is projected from (2,0,0) that is from the ground.
Initial velocity= u= 10 m/s
Angle of projection, \[\theta ={{45}^{0}}\]
A horizontal line PQ which makes an angle \[\theta ={{37}^{0}}\]
Range, \[R=\dfrac{{{u}^{2}}\sin 2\theta }{g}\]
Putting the values, we get
\[
 R=\dfrac{{{10}^{2}}\sin 90}{10} \\
\Rightarrow R=10m \\
\]
So, the x coordinate will be \[10\cos {{37}^{0}}+2=10\]
And y coordinate will be \[10\sin {{37}^{0}}=6\]
And the z coordinate will be 0.

So, the correct option must be in the form of (10,6,0) and this matches with option (A).

Note: In projectile problems when the body is projected whether, from the ground or a certain height, there is no acceleration in the horizontal direction. There is constant acceleration in the vertical direction which is always directed downwards and this is constant. This is the acceleration due to gravity.