Question

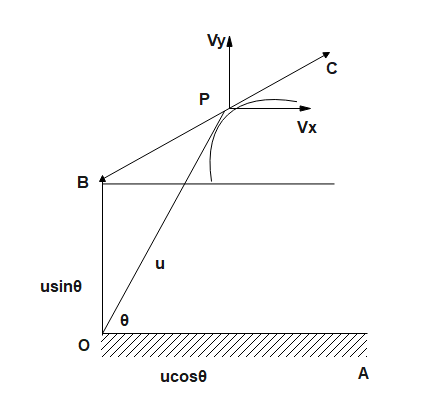
A particle is projected from a point $O$ in the horizontal surface \[OA\] with speed $u$ and angle of projection $\theta$. It just grazes the plane \[BC\] which makes an angle $\alpha$ with the horizontal. The time taken by the projectile to reach $p$ from the instant of projection is:

Answer 1

Hint: The flight time is called the time it takes for an object to be projected and land. It relies on the projectile's initial velocity and the projection angle. The projectile's maximum height is when the projectile reaches zero vertical velocity. Calculate velocity in X and Y direction respectively and take the ratio Then calculate

Formula used:
$\text{t}=\dfrac{\text{u}[\sin \theta -\tan \alpha \cos \theta ]}{\text{g}}$

Complete Step-by-Step solution:
A projectile is an object given an initial velocity, and gravity acts on it. The amount of time it spends in the air is referred to as flight time.

From figure: $\quad \mathrm{u}_{\mathrm{x}}=\mathrm{u} \cos \theta \quad \mathrm{u}_{\mathrm{y}}=\mathrm{usin} \theta$

At point $\mathrm{P}$, the particle just grazes the line $\mathrm{BC}$ at the instant
$\mathrm{t}$ i.e. $\dfrac{\mathrm{V}_{\mathrm{y}}}{\mathrm{V}_{\mathrm{x}}}=\tan \alpha$
Also, as
${{a}_{x}}=0$
${{V}_{x}}={{u}_{x}}=u\cos \theta $
$\therefore \mathrm{V}_{\mathrm{y}}=\mathrm{V}_{\mathrm{x}} \tan \alpha=(\mathrm{u} \cos \theta) \tan \alpha$

$\mathrm{y}$ direction $: \quad \mathrm{V}_{\mathrm{y}}=\mathrm{u}_{\mathrm{y}}-\mathrm{gt}$
$\therefore \quad \mathrm{u} \cos \theta \tan \alpha=\operatorname{usin} \theta-\mathrm{gt}$
OR
$\quad \mathrm{t}=\dfrac{\mathrm{u}[\sin \theta-\tan \alpha \cos \theta]}{\mathrm{g}}=\dfrac{\mathrm{u}[\sin \theta \cos \alpha-\sin \alpha \cos \theta]}{\operatorname{gcos} \alpha}$
$\therefore \text{t}=\dfrac{\text{usin}(\theta -\alpha )}{\text{g}\cos \alpha }$

The time taken by the projectile to reach $p$ from the instant of projection is $\dfrac{\text{usin}(\theta -\alpha )}{\text{g}\cos \alpha }$

Note:
The horizontal displacement of the projectile is called the projectile range and is dependent on the object's initial velocity. In a bilaterally symmetrical, parabolic path, projectile motion is a form of motion in which an object moves. Its trajectory is called the path that the object follows. Projectile motion occurs only when one force is applied to the trajectory at the beginning, after which the only interference is from gravity. A projectile motion's flight time is exactly what it sounds like. It is the moment from which the object is projected to the moment the surface is reached.