Question

A particle is placed at rest inside a hollow hemisphere of radius $R$. The coefficient of friction between the particle and the hemisphere is $\mu = \dfrac{1}{{\sqrt 3 }}$ . the maximum height up to which the particle can remain stationary is
\[(A)\dfrac{R}{2}\]
\[(B)\left( {1 - \dfrac{{\sqrt 3 }}{2}} \right)R\]
\[(C)\dfrac{{\sqrt 3 }}{2}R\]
\[(D)\dfrac{{3R}}{8}\]

Answer 1

Hint: The free-body diagram has to be drawn to show the applied forces on the given particle. The forces have to be divided into components as per requirements. The amount of the limiting friction will be the frictional coefficient times radius of the sphere. After equating the forces that are equally applied on the particle the value of the tangent of the angle (in which the forces are divided into components) can be found. From this value, the maximum height up to which the particle can remain stationary can be calculated.

Formula used:
The limiting friction $F = \mu N$ , $\mu $ is the coefficient of friction between the particle and the hemisphere.
$N$ is the normal reaction force of the sphere on the particle.
$N = mg\cos \theta $ , $mg\cos \theta $ is the horizontal component of the weight of the particle $mg$ .
The height \[h = R - R\cos \theta \] , \[R\] is the radius of the sphere.

Complete step by step solution:
Let the particle of mass \[m\] stay at rest on the point \[B\] w.r…t the point\[A\] .
The point \[B\] is at height \[h\] .
 

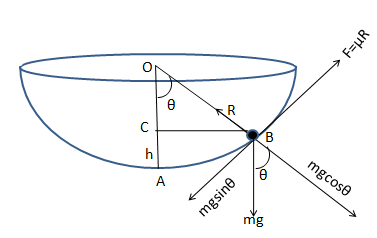
The horizontal component of the weight of the particle along the radius is $mg\cos \theta $. Hence the normal reaction force of the sphere on the particle $N = mg\cos \theta $.
The vertical component of the weight $mg\sin \theta $ tries to move the particle.
The limiting friction $F = \mu N$ , $\mu $ is the coefficient of friction between the particle and the hemisphere.
The condition for staying at the rest is that these two forces have to eliminate each other.
i.e. $mg\sin \theta = \mu mg\cos \theta $
$ \Rightarrow \tan \theta = \mu $
Given that, $\mu = \dfrac{1}{{\sqrt 3 }}$
$\therefore \tan \theta = \mu $
$ \Rightarrow \tan \theta = \dfrac{1}{{\sqrt 3 }}$
$ \Rightarrow \theta = {30^ \circ }$
Now, from the diagram $\Delta OBC \Rightarrow OC = OB\cos 30^\circ $
$ \Rightarrow OC = R\dfrac{{\sqrt 3 }}{2}$ [since, the radius of the sphere $OB = R$ ]
Now, The height $h = AC = AO - OC$
$ \Rightarrow h = R - \dfrac{{\sqrt 3 R}}{2}$ [ also, we can write $h = R - R\cos \theta $ ]
\[ \Rightarrow h = R\left( {1 - \dfrac{{\sqrt 3 }}{2}} \right)\]
Hence, the maximum height up to which the particle can remain stationary is \[ \Rightarrow h = R\left( {1 - \dfrac{{\sqrt 3 }}{2}} \right)\]


Note:Here we can know about a term called ‘limiting friction’. When the amount of the applied force along the horizontal axis, the value of static friction ( the friction that tries to stop a particle from a movement) also increases slowly and reaches a maximum value. That means, there is also a limit in the increase of the friction by itself. The applied force when greater than the limit, the particle can not remain at rest. This maximum value of the static friction is known as the limiting friction or limiting value of static friction. After that, with the increase of the applied force, the value of the friction can not increase.