Question

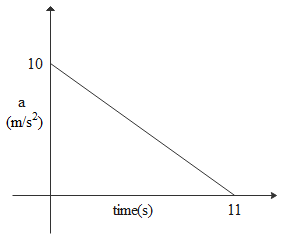
A particle is initially at rest, it is subjected to a linear acceleration a, as shown in the figure. The maximum speed attained by the particle is

A. ${\text{605 }}m/s$
B. ${\text{110 }}m/s$
C. ${\text{55 }}m/s$
D. ${\text{550 }}m/s$

Answer 1

Hint: Velocity is rate of change of displacement with respect to the time. For a particular path we can define instantaneous velocity and average velocity. Velocity at a particular time instant is called instantaneous velocity and velocity over a certain duration of time is average velocity. Here we have to find a time instant where velocity becomes maximum and find out velocity there.
Formula used:
$\eqalign{
  & a = \dfrac{{dv}}{{dt}} \cr
  & v = \int {(a)} dt \cr} $

Complete answer:
Acceleration is the rate of change of the velocity. Both velocity and acceleration are the vectors.
$a = \dfrac{{dv}}{{dt}}$ where ‘a’ is an acceleration and ‘v’ is the velocity and ‘t’ is the time
If we integrate velocity with respect to time we then get acceleration of an object. Now differentiation gives us the slope of the particular graph while integration gives us the area under the particular graph. If there is graph between velocity and time then area under that graph gives us the displacement while if there is a plot between velocity and time then area under that plot will give us the acceleration
$v = \int {(a)} dt$

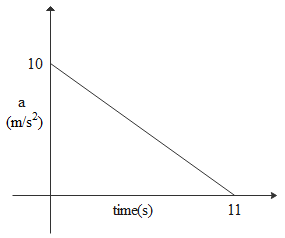
If we look at the graph carefully with its plot between acceleration and the time, acceleration is always positive and initial velocity is zero. Hence object velocity will be positive that will move in only one direction. Until its acceleration becomes zero the body keeps on moving in the same direction with increasing velocity i.e until 11seconds in this plot.
So area of this triangle will be $0.5 \times 11 \times 10 = 55m/s$

So, the correct answer is “Option C”.

Note:
There is another way we can solve this problem. We find the acceleration as a function of time and integrate it to get velocity. Now substitute the time value where acceleration is zero and then we will get the maximum velocity. Area method will be a bit easier than this integration method.