Question

A particle is in motion along a circle of radius $\left( \dfrac{20}{\pi }m \right)$ with a fixed tangential acceleration. Suppose the velocity of the particle is \[80m{{s}^{-1}}\] at the end of second revolution after the motion has started, the tangential acceleration will be:
$\begin{align}
  & A.\quad 40\pi m{{s}^{-2}} \\
 & B.\quad 40m{{s}^{-2}} \\
 & C.\quad 160\pi m{{s}^{-2}} \\
 & D.\quad 640\pi m{{s}^{-2}} \\
\end{align}$

Answer 1

Hint: First of all we have to convert the linear variables such as linear displacement, linear velocity, and linear acceleration to the circular variables of angular displacement, angular velocity and angular acceleration. Then the initial tangential acceleration should be found. The difference of the squares of the angular velocities will be equivalent to the twice of the product of angular acceleration and angular displacement. Using this the angular acceleration is found, then we can find the required value of the tangential acceleration.

Complete step by step answer:

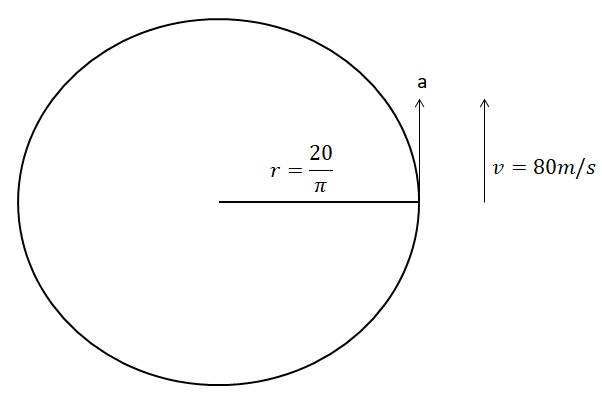
We have a circle of radius $\left( \dfrac{20}{\pi }m \right)$. A body is moving in the circle, with constant tangential acceleration $\left( a \right)$. At the end of second revolution of the circle, the tangential velocity of the body is given as \[80m{{s}^{-1}}\], that is \[v=80m{{s}^{-1}}\].
Let’s first establish the relation between the linear motion variables and the circular motion variables. The relation between linear displacement $\left( s \right)$ and the angular displacement \[(\theta )\] is given by,
$\theta =\dfrac{s}{r}\approx \dfrac{arc}{r}$
Hence, the angular displacement is equal to the linear distance traversed in the form of an arc around a circle of radius $\left( r \right)$ divided by the radius of the circle $\left( r \right)$.
The relation between the linear velocity $\left( v \right)$ and the angular velocity \[(\omega )\] can be written as,
$v=\dfrac{s}{t}$.
 Substituting in the value of linear displacement from above it becomes,
$\begin{align}
  & v=\dfrac{s}{t}=\dfrac{\theta .r}{t} \\
 & \Rightarrow v=\dfrac{\theta }{t}(r) \\
 & \Rightarrow v=\omega r \\
\end{align}$
Since, $\dfrac{\theta }{t}$ is equal to angular velocity \[(\omega )\].
The relation between the linear acceleration $\left( a \right)$ and the angular acceleration $\left( \alpha \right)$ is very simple. The linear acceleration is equal to angular acceleration times the radius.
 Here is the explanation,
$\begin{align}
  & a=\dfrac{{{v}_{2}}-{{v}_{1}}}{t} \\
 & \Rightarrow a=\dfrac{{{\omega }_{2}}r-{{\omega }_{1}}r}{t}=\dfrac{{{\omega }_{2}}-{{\omega }_{1}}}{t}(r) \\
 & \Rightarrow a=\alpha r \\
\end{align}$
Using these, we convert the linear formula of:
${{v}^{2}}-{{u}^{2}}=2as$
To:
${{\omega }^{2}}-\omega _{0}^{2}=2\alpha \theta $
Let us take the particle to be at rest initially.
Hence $u=0$, that is
${{\omega }_{0}}=0$
Therefore,
$\begin{align}
  & {{\omega }^{2}}-\omega _{0}^{2}=2\alpha \theta \\
 & \Rightarrow {{(\dfrac{v}{r})}^{2}}-{{0}^{2}}=2\dfrac{a}{r}\theta \\
\end{align}$.
The final tangential velocity is
\[v=80m{{s}^{-1}}\]
After 2 revolutions, hence the linear distance is twice the perimeter. Hence,
$\begin{align}
  & {{(\dfrac{80}{r})}^{2}}=2\dfrac{a}{r}\dfrac{2\times 2\pi r}{r} \\
 & \Rightarrow 6400=8\pi ra \\
\end{align}$
Substituting in the value of the radius $(\dfrac{20}{\pi })m$, we find the value of a to be,
$\begin{align}
  & 6400=8\pi (\dfrac{20}{\pi })a \\
 & \Rightarrow a=\dfrac{6400}{160} \\
 & \Rightarrow a=40m{{s}^{-2}} \\
\end{align}$
Therefore, the value of the constant tangential acceleration is
$a=40m{{s}^{-2}}$
It is given as option B.

Note:
An alternate method of solving the problem is,
We will first the amount of distance covered in two revolutions for the radius
$r=\dfrac{20}{\pi }m$.
Therefore, distance s is,
$\begin{align}
  & s=2\times 2\pi r=2(2\pi \times \dfrac{20}{\pi })m \\
 & \Rightarrow s=80m \\
\end{align}$
For the particle starting from rest, that is $u=0$, the newton’s law of motion states,
$\begin{align}
  & {{v}^{2}}-{{u}^{2}}=2as \\
 & \Rightarrow {{v}^{2}}=2as \\
 & \Rightarrow a=\dfrac{{{v}^{2}}}{2s} \\
\end{align}$
Hence putting in the value of final tangential velocity as \[v=80m{{s}^{-1}}\], we get,
$\begin{align}
  & a=\dfrac{{{v}^{2}}}{2s} \\
 & \Rightarrow a=\dfrac{{{(80)}^{2}}}{2(80)} \\
 & \therefore a=40m{{s}^{-2}} \\
\end{align}$