
A particle is executing simple harmonic motion (SHM) of amplitude $A$, along the x-axis, about $x = 0$. When its potential energy (PE) equals kinetic energy (KE), the position of the particle will be:
(A) $\dfrac{A}{2}$
(B) $\dfrac{A}{{2\sqrt 2 }}$
(C) $\dfrac{A}{{\sqrt 2 }}$
(D) $A$
Answer
579.3k+ views
Hint
To solve this question, we have to assume the required position in the form of a variable. Then, on equating the kinetic energy and the potential energy at that point, we will get the required position.
The formulae used to solve this question are:
$\Rightarrow U = \dfrac{1}{2}m{\omega ^2}{x^2}$
$\Rightarrow K = \dfrac{1}{2}m{\omega ^2}({A^2} - {x^2})$
$U$ and $K$ are the respective potential and kinetic energies of a particle of mass $m$ executing a simple harmonic motion of angular frequency $\omega $ and amplitude $A$ about $x = 0.$
Complete step by step answer
The oscillation of the particle is shown in the below figure. Let $\omega $ be the angular frequency of the simple harmonic motion of the particle and$m$be the mass of the particle.
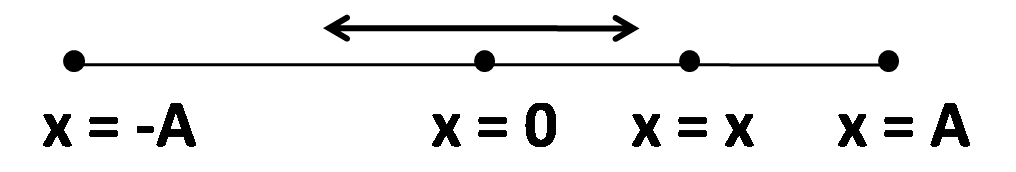
Here, the origin is fixed at the mean position, according to the question.
Let x be the position of the particle, where the potential energy and the kinetic energy of the particle are equal.
Now, as we know, the potential energy at this point is
$\Rightarrow U = \dfrac{1}{2}m{\omega ^2}{x^2}$
And, the kinetic energy at this point is
$\Rightarrow K = \dfrac{1}{2}m{\omega ^2}({A^2} - {x^2})$
According to the question
$\Rightarrow U = K$
$\therefore \dfrac{1}{2}m{\omega ^2}{x^2} = \dfrac{1}{2}m{\omega ^2}({A^2} - {x^2})$
Cancelling $\dfrac{1}{2}m{\omega ^2}$ from both the sides, we get
$\Rightarrow {x^2} = {A^2} - {x^2}$
Adding ${x^2}$ both sides
$\Rightarrow 2{x^2} = {A^2}$
$\Rightarrow {x^2} = \dfrac{{{A^2}}}{2}$
On solving this quadratic equation, we get
$\Rightarrow x = \pm \dfrac{A}{{\sqrt 2 }}$
Now, we see that $x = - \dfrac{A}{{\sqrt 2 }}$ is not in the options. Therefore we reject it.
So, the final value is $x = \dfrac{A}{{\sqrt 2 }}$
Hence, the correct answer is option (C), $\dfrac{A}{{\sqrt 2 }}$.
Note
In the last quadratic equation formed, don’t forget to write the negative root. We generally have the habit of taking only the positive root in these types of quadratic equations, where the coefficient of the variable $x$ is equal to zero. In this question, two answers are possible. One answer is given by the positive root, and the other is given by the negative root. The latter is not in the options. Because of this, we have rejected it.
To solve this question, we have to assume the required position in the form of a variable. Then, on equating the kinetic energy and the potential energy at that point, we will get the required position.
The formulae used to solve this question are:
$\Rightarrow U = \dfrac{1}{2}m{\omega ^2}{x^2}$
$\Rightarrow K = \dfrac{1}{2}m{\omega ^2}({A^2} - {x^2})$
$U$ and $K$ are the respective potential and kinetic energies of a particle of mass $m$ executing a simple harmonic motion of angular frequency $\omega $ and amplitude $A$ about $x = 0.$
Complete step by step answer
The oscillation of the particle is shown in the below figure. Let $\omega $ be the angular frequency of the simple harmonic motion of the particle and$m$be the mass of the particle.
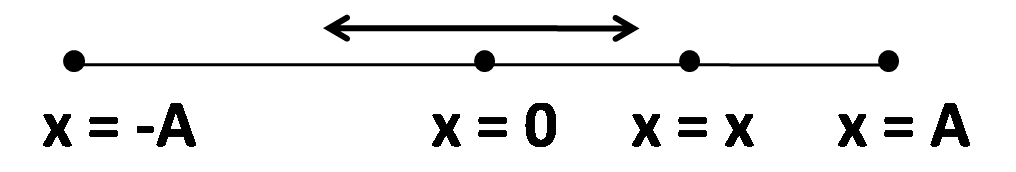
Here, the origin is fixed at the mean position, according to the question.
Let x be the position of the particle, where the potential energy and the kinetic energy of the particle are equal.
Now, as we know, the potential energy at this point is
$\Rightarrow U = \dfrac{1}{2}m{\omega ^2}{x^2}$
And, the kinetic energy at this point is
$\Rightarrow K = \dfrac{1}{2}m{\omega ^2}({A^2} - {x^2})$
According to the question
$\Rightarrow U = K$
$\therefore \dfrac{1}{2}m{\omega ^2}{x^2} = \dfrac{1}{2}m{\omega ^2}({A^2} - {x^2})$
Cancelling $\dfrac{1}{2}m{\omega ^2}$ from both the sides, we get
$\Rightarrow {x^2} = {A^2} - {x^2}$
Adding ${x^2}$ both sides
$\Rightarrow 2{x^2} = {A^2}$
$\Rightarrow {x^2} = \dfrac{{{A^2}}}{2}$
On solving this quadratic equation, we get
$\Rightarrow x = \pm \dfrac{A}{{\sqrt 2 }}$
Now, we see that $x = - \dfrac{A}{{\sqrt 2 }}$ is not in the options. Therefore we reject it.
So, the final value is $x = \dfrac{A}{{\sqrt 2 }}$
Hence, the correct answer is option (C), $\dfrac{A}{{\sqrt 2 }}$.
Note
In the last quadratic equation formed, don’t forget to write the negative root. We generally have the habit of taking only the positive root in these types of quadratic equations, where the coefficient of the variable $x$ is equal to zero. In this question, two answers are possible. One answer is given by the positive root, and the other is given by the negative root. The latter is not in the options. Because of this, we have rejected it.
Recently Updated Pages
Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

There are 720 permutations of the digits 1 2 3 4 5 class 11 maths CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE




