Question

A particle is constrained to move in a circle with a 10-meter radius. At one instant, the particle’s speed is \[10\,{\text{m/s}}\] and is increasing at a rate of \[10\,{\text{m/}}{{\text{s}}^2}\]. The angle between the particle’s velocity and acceleration vectors is
A.\[0^\circ \]
B.\[30^\circ \]
C.\[45^\circ \]
D.\[60^\circ \]

Answer 1

Hint: Use the formula for the radial acceleration of the particle in circular motion.
Also use the formula for the angle made by the acceleration vector with the components of acceleration.

Formula used:
The radial component \[{a_r}\] of acceleration of a particle in circular motion is given by
\[{a_r} = \dfrac{{{v^2}}}{r}\] …… (1)
Here, \[v\] is the velocity of the particle and \[r\] is the radius of the circle.
The angle \[\theta \] made by the resultant acceleration vector is
\[\theta = {\tan ^{ - 1}}\left( {\dfrac{{{a_r}}}{{{a_t}}}} \right)\] …… (2)
Here, \[{a_t}\] is the tangential component of acceleration and \[{a_r}\] is the radial component of acceleration.

Complete step by step answer:
The particle is moving in a circle of radius \[10\,{\text{m}}\].
The instantaneous speed \[v\] of the particle is \[10\,{\text{m/s}}\] and is increasing at a rate of \[10\,{\text{m/}}{{\text{s}}^2}\].
\[v = 10\,{\text{m/s}}\]
Hence, the tangential acceleration \[{a_t}\] of the particle is \[10\,{\text{m/}}{{\text{s}}^2}\].
\[{a_t} = 10\,{\text{m/}}{{\text{s}}^2}\]
The directions of the velocity, tangential and radial acceleration of the particle in the circular motion is as follows:

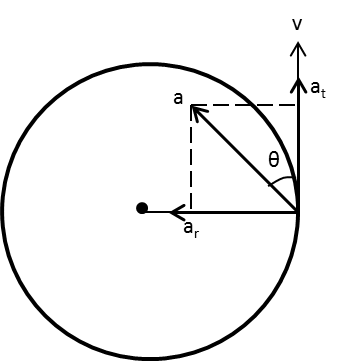
Calculate the radial acceleration of the particle.
Substitute \[10\,{\text{m/s}}\] for \[v\] and \[10\,{\text{m}}\] for \[r\] in equation (1).
\[{a_r} = \dfrac{{{{\left( {10\,{\text{m/s}}} \right)}^2}}}{{10\,{\text{m}}}}\]
\[ \Rightarrow {a_r} = 10\,{\text{m/}}{{\text{s}}^2}\]
Hence, the radial acceleration of the particle is \[10\,{\text{m/}}{{\text{s}}^2}\].
Calculate the angle made by the resultant acceleration of the particle with the velocity vector.
Substitute \[10\,{\text{m/}}{{\text{s}}^2}\] for \[{a_r}\] and \[10\,{\text{m/}}{{\text{s}}^2}\] for \[{a_t}\] in equation (2).
\[\theta = {\tan ^{ - 1}}\left( {\dfrac{{10\,{\text{m/}}{{\text{s}}^2}}}{{10\,{\text{m/}}{{\text{s}}^2}}}} \right)\]
\[ \Rightarrow \theta = {\tan ^{ - 1}}\left( 1 \right)\]
\[ \Rightarrow \theta = 45^\circ \]
Hence, the angle made by the resultant acceleration vector with the components of acceleration (tangential acceleration) is \[45^\circ \].
Therefore, the angle between the acceleration and velocity vectors is \[45^\circ \].

So, the correct answer is “Option C”.

Note:
The rate of change of instantaneous velocity is \[10\,{\text{m/}}{{\text{s}}^2}\].
Hence, the acceleration \[10\,{\text{m/}}{{\text{s}}^2}\] is the tangential acceleration.
Calculate the angle made by the resultant acceleration of the particle with the velocity vector.